
ЎҫМвДҝЎҝОӘБЛјмІвЙъІъПЯЙПДіЦЦБгјюөДЦКБҝЈ¬ҙУІъЖ·ЦРЛж»ъійИЎ100ёцБгјюЈ¬ІвБҝЖдіЯҙзЈ¬өГөҪИзНјЛщКҫөДЖөВК·ЦІјЦұ·ҪНјЈ®ИфБгјюіЯҙзВдФЪЗшјд![]() Ц®ДЪЈ¬ФтИПОӘёГБгјюәПёсЈ¬·сФтИПОӘІ»әПёсЈ®ЖдЦР
Ц®ДЪЈ¬ФтИПОӘёГБгјюәПёсЈ¬·сФтИПОӘІ»әПёсЈ®ЖдЦР![]() Ј¬
Ј¬![]() ·ЦұрұнКҫСщұҫөДЖҪҫщЦөәНұкЧјІоЈ¬јЖЛгөГ
·ЦұрұнКҫСщұҫөДЖҪҫщЦөәНұкЧјІоЈ¬јЖЛгөГ![]() ЈЁН¬Т»ЧйЦРөДКэҫЭУГёГЧйЗшјдөДЦРөгЦөЧчҙъұнЈ©Ј®
ЈЁН¬Т»ЧйЦРөДКэҫЭУГёГЧйЗшјдөДЦРөгЦөЧчҙъұнЈ©Ј®
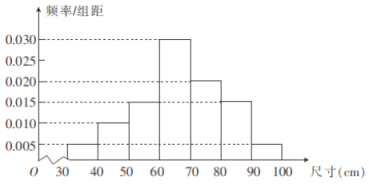
ЈЁ1Ј©ТСЦӘТ»ёцБгјюөДіЯҙзКЗ![]() Ј¬КФЕР¶ПёГБгјюКЗ·сәПёсЈ»
Ј¬КФЕР¶ПёГБгјюКЗ·сәПёсЈ»
ЈЁ2Ј©АыУГ·ЦІгійСщөД·Ҫ·ЁҙУіЯҙзФЪ![]() өДСщұҫЦРійИЎ6ёцБгјюЈ¬ФЩҙУХв6ёцБгјюЦРЛж»ъійИЎ2ёцЈ¬ЗуХв2ёцБгјюЦРЗЎУР1ёціЯҙзРЎУЪ
өДСщұҫЦРійИЎ6ёцБгјюЈ¬ФЩҙУХв6ёцБгјюЦРЛж»ъійИЎ2ёцЈ¬ЗуХв2ёцБгјюЦРЗЎУР1ёціЯҙзРЎУЪ![]() өДёЕВКЈ®
өДёЕВКЈ®
Ўҫҙр°ёЎҝЈЁ1Ј©ёГБгјюІ»әПёсЈ®ЈЁ2Ј©![]()
ЎҫҪвОцЎҝ
ЈЁ1Ј©ёщҫЭЖөВК·ЦІјЦұ·ҪНјЈ¬јЖЛгіц![]() өДЗшјдЈ¬ФЩЕР¶П
өДЗшјдЈ¬ФЩЕР¶П![]() КЗ·сКфУЪЗшјдДЪЈ¬јҙҝЙөГҙр°ёЈ»
КЗ·сКфУЪЗшјдДЪЈ¬јҙҝЙөГҙр°ёЈ»
ЈЁ2Ј©јЗХв6ёцБгјюұаәЕОӘЈә![]() Ј¬ФЩБРіцҙУХв6ёцБгјюЦРЛж»ъійИЎ2ёцөД»щұҫКВјюЈ¬јЗКВјю
Ј¬ФЩБРіцҙУХв6ёцБгјюЦРЛж»ъійИЎ2ёцөД»щұҫКВјюЈ¬јЗКВјю![]() ОӘЈәЎ°СЎіцөД2ёцБгјюЦРЗЎУР1ёціЯҙзРЎУЪ
ОӘЈәЎ°СЎіцөД2ёцБгјюЦРЗЎУР1ёціЯҙзРЎУЪ![]() ЎұЈ¬јЖЛгКВјю
ЎұЈ¬јЖЛгКВјю![]() °ьә¬өД»щұҫКВјюЈ¬АыУГ№ЕөдёЕРНјЖЛгёЕВКЈ¬јҙҝЙөГҙр°ёЈ»
°ьә¬өД»щұҫКВјюЈ¬АыУГ№ЕөдёЕРНјЖЛгёЕВКЈ¬јҙҝЙөГҙр°ёЈ»
ЈЁ1Ј©јЗёчЧйөДЖөВКОӘ![]() Ј¬ТАМвТвөГ
Ј¬ТАМвТвөГ
![]() Ј¬
Ј¬
![]()
Ўа![]()
![]()
Ўа![]()
¶ш![]() Ј¬№КёГБгјюІ»әПёсЈ®
Ј¬№КёГБгјюІ»әПёсЈ®
ЈЁ2Ј©јЗЗ°ИэЧйійИЎөДБгјюёцКэ·ЦұрОӘ![]()
Ўа![]() Ј¬Ўа
Ј¬Ўа![]()
ЎаійИЎіцөД6ёцБгјюЦРіЯҙзРЎУЪ![]() өДУР3ёцЈ®
өДУР3ёцЈ®
јЗХв6ёцБгјюұаәЕОӘЈә![]() ЈЁЖдЦР
ЈЁЖдЦР![]() ОӘіЯҙзРЎУЪ
ОӘіЯҙзРЎУЪ![]() өДЈ©
өДЈ©
јЗКВјю![]() ОӘЈәЎ°СЎіцөД2ёцБгјюЦРЗЎУР1ёціЯҙзРЎУЪ
ОӘЈәЎ°СЎіцөД2ёцБгјюЦРЗЎУР1ёціЯҙзРЎУЪ![]() Ўұ
Ўұ
ЎаҙУХв6ёцБгјюЦРЛж»ъійИЎ2ёцөД»щұҫКВјюУРЈә
![]()
![]() №І15ёцЈ®
№І15ёцЈ®
ФтКВјю![]() °ьә¬өД»щұҫКВјюУРЈә
°ьә¬өД»щұҫКВјюУРЈә
![]() №І9ёц
№І9ёц
Ўа![]()
ЎаХв2ёцБгјюЦРЗЎУР1ёціЯҙзРЎУЪ![]() өДёЕВКОӘ
өДёЕВКОӘ![]() Ј®
Ј®


 РВЛјО¬јЩЖЪЧчТөә®јЩјӘБЦҙуС§іц°жЙзПөБРҙр°ё
РВЛјО¬јЩЖЪЧчТөә®јЩјӘБЦҙуС§іц°жЙзПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪЦұИэАвЦщ![]() ЦРЈ¬
ЦРЈ¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() ·ЦұрКЗ
·ЦұрКЗ![]() Ј¬
Ј¬![]() ЦРөгЈ¬
ЦРөгЈ¬![]() ОӘПЯ¶О
ОӘПЯ¶О![]() ЙПөДТ»ёц¶Ҝөг.
ЙПөДТ»ёц¶Ҝөг.
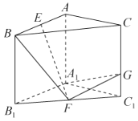
ЈЁ1Ј©ЦӨГчЈә![]() ЖҪГж
ЖҪГж![]() Ј»
Ј»
ЈЁ2Ј©өұ¶юГжҪЗ![]() өДУаПТЦөОӘ
өДУаПТЦөОӘ![]() КұЈ¬ЦӨГчЈә
КұЈ¬ЦӨГчЈә![]() .
.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘәҜКэ![]() ЈЁ
ЈЁ![]() Ј¬
Ј¬![]() ОӘЧФИ»¶ФКэөДөЧКэЈ©.
ОӘЧФИ»¶ФКэөДөЧКэЈ©.
ЈЁ1Ј©ИфәҜКэ![]() ФЪөг
ФЪөг![]() ҙҰөДЗРПЯөДРұВКОӘ
ҙҰөДЗРПЯөДРұВКОӘ![]() Ј¬ЗуКөКэ
Ј¬ЗуКөКэ![]() өДЦөЈ»
өДЦөЈ»
ЈЁ2Ј©өұ![]() КұЈ¬МЦВЫәҜКэ
КұЈ¬МЦВЫәҜКэ![]() өДөҘөчРФЈ»
өДөҘөчРФЈ»
ЈЁ3Ј©Иф№ШУЪ![]() өДІ»өИКҪ
өДІ»өИКҪ![]() ФЪЗшјд
ФЪЗшјд![]() ЙПәгіЙБўЈ¬ЗуКөКэ
ЙПәгіЙБўЈ¬ЗуКөКэ![]() өДИЎЦө·¶О§.
өДИЎЦө·¶О§.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝЙПКАјНД©әУДПіцНБөДТФәЧөДіЯ№ЗЈЁіб№ЗЈ©ЦЖіЙөДЎ°№ЗөСЎұЈЁНј1Ј©Ј¬ід·ЦХ№КҫБЛОТ№ъ№ЕҙъёЯі¬өДТфВЙТХКхј°ПИҪшөДКэС§Л®ЖҪЈ¬ТІУЎЦӨБЛОТ№ъ№ЕҙъТфВЙУлАъ·ЁөДГЬЗРБӘПө.Нј2ОӘ№ЗөСІвБҝЎ°ҙәЈЁЗпЈ©·ЦЎұЈ¬Ў°ПДЈЁ¶¬Ј©ЦБЎұөДКҫТвНјЈ¬Нј3КЗДі№ЗөСөДІҝ·ЦІвБҝКэҫЭЈЁ№ЗөСөДНдЗъәцВФІ»јЖЈ©Ј¬ПДЦБЈЁ»т¶¬ЦБЈ©ИХ№вЈЁөұИХХэОзМ«Сф№вПЯЈ©УлҙәЗп·ЦИХ№вЈЁөұИХХэОзМ«Сф№вПЯЈ©өДјРҪЗөИУЪ»ЖіаҪ»ҪЗ.

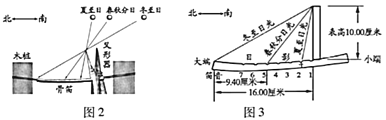
УЙАъ·ЁАнВЫЦӘЈ¬»ЖіаҪ»ҪЗҪь1НтДкіЦРшјхРЎЈ¬ЖдХэЗРЦөј°¶ФУҰөДДкҙъИзПВұнЈә
»ЖіаҪ»ҪЗ |
|
|
|
|
|
ХэЗРЦө | 0.439 | 0.444 | 0.450 | 0.455 | 0.461 |
Дкҙъ | №«ФӘФӘДк | №«ФӘЗ°2000Дк | №«ФӘЗ°4000Дк | №«ФӘЗ°6000Дк | №«ФӘЗ°8000Дк |
ёщҫЭТФЙПРЕПўЈ¬НЁ№эјЖЛг»ЖіаҪ»ҪЗЈ¬ҝЙ№АјЖёГ№ЗөСөДҙуЦВДкҙъКЗ( )
A.№«ФӘЗ°2000ДкөҪ№«ФӘФӘДкB.№«ФӘЗ°4000ДкөҪ№«ФӘЗ°2000Дк
C.№«ФӘЗ°6000ДкөҪ№«ФӘЗ°4000ДкD.ФзУЪ№«ФӘЗ°6000Дк
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪіӨ·ҪМеABCD©ҒA1B1C1D1ЦРЈ¬AA1ЈҪ8Ј¬ABЈҪ3Ј¬ADЈҪ8Ј¬өгMКЗАвADөДЦРөгЈ¬өгNКЗАвAA1өДЦРөгЈ¬PКЗІаГжЛДұЯРОADD1A1ДЪТ»¶ҜөгЈЁә¬ұЯҪзЈ©Ј¬ИфC1PЎОЖҪГжCMNЈ¬ФтПЯ¶ОC1PіӨ¶ИөДИЎЦө·¶О§КЗЈЁЎЎЎЎЈ©
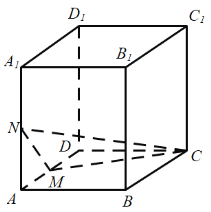
A.![]() B.[4Ј¬5]C.[3Ј¬5]D.
B.[4Ј¬5]C.[3Ј¬5]D.![]()
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝДі№Өі§јЖ»®ҪЁЙиЦБЙЩ3ёцЈ¬ЦБ¶а5ёцПаН¬өДЙъІъПЯіөјдЈ¬ТФҪвҫцұҫөШЗш№«Гс¶ФМШ№©ЙМЖ·![]() өДОҙАҙРиЗуЈ®ҫӯ№э¶ФПИЖЪСщұҫөДҝЖС§РФөчІйПФКҫЈ¬ұҫөШЗшГҝёцФВ¶ФЙМЖ·
өДОҙАҙРиЗуЈ®ҫӯ№э¶ФПИЖЪСщұҫөДҝЖС§РФөчІйПФКҫЈ¬ұҫөШЗшГҝёцФВ¶ФЙМЖ·![]() өДФВРиЗуБҝҫщФЪ50Нтјюј°ТФЙПЈ¬ЖдЦРРиЗуБҝФЪ50~ 100НтјюөДЖөВКОӘ0.5Ј¬РиЗуБҝФЪ100~200НтјюөДЖөВКОӘ0.3Ј¬І»өНУЪ200НтјюөДЖөВКОӘ0.2Ј®УГөчІйСщұҫАҙ№АјЖЧЬМеЈ¬ЖөВКЧчОӘПаУҰ¶ОөДёЕВКЈ¬ІўјЩЙиұҫөШЗшФЪёчёцФВ¶ФұҫМШ№©ЙМЖ·
өДФВРиЗуБҝҫщФЪ50Нтјюј°ТФЙПЈ¬ЖдЦРРиЗуБҝФЪ50~ 100НтјюөДЖөВКОӘ0.5Ј¬РиЗуБҝФЪ100~200НтјюөДЖөВКОӘ0.3Ј¬І»өНУЪ200НтјюөДЖөВКОӘ0.2Ј®УГөчІйСщұҫАҙ№АјЖЧЬМеЈ¬ЖөВКЧчОӘПаУҰ¶ОөДёЕВКЈ¬ІўјЩЙиұҫөШЗшФЪёчёцФВ¶ФұҫМШ№©ЙМЖ·![]() өДРиЗуПа»Ҙ¶АБўЈ®
өДРиЗуПа»Ҙ¶АБўЈ®
ЈЁ1Ј©ЗуФЪОҙАҙДіБ¬Рш4ёцФВЦРЈ¬ұҫөШЗшЦБЙЩУР2ёцФВ¶ФЙМЖ·![]() өДФВРиЗуБҝөНУЪ100НтјюөДёЕВКЈ®
өДФВРиЗуБҝөНУЪ100НтјюөДёЕВКЈ®
ЈЁ2Ј©ёГ№Өі§ПЈНыҫЎҝЙДЬФЪЙъІъПЯіөјдҪЁіЙәуЈ¬іөјдДЬХэіЈЙъІъФЛРРЈ¬ө«ГҝФВЧо¶аҝЙХэіЈЙъІъөДіөјдКэКЬЙМЖ·![]() өДРиЗуБҝ
өДРиЗуБҝ![]() өДПЮЦЖЈ¬ІўУРИзПВ№ШПөЈә
өДПЮЦЖЈ¬ІўУРИзПВ№ШПөЈә
ЙМЖ· |
|
|
|
іөјдЧо¶аХэіЈФЛРРёцКэ | 3 | 4 | 5 |
ИфТ»ёціөјдХэіЈФЛРРЈ¬ФтёГіөјдФВҫ»АыИуОӘ1500НтФӘЈ¬¶шТ»ёціөјдОҙХэіЈЙъІъЈ¬ФтёГіөјдЙъІъПЯөДФВО¬»Ө·СЈЁөҘО»ЈәНтФӘЈ©УлФВРиЗуБҝУРИзПВ№ШПөЈә
ЙМЖ· |
|
|
ОҙХэіЈЙъІъөДТ»ёціөјдөДФВО¬»Ө·СЈЁНтФӘЈ© | 500 | 600 |
КФ·ЦОцІў»ШҙрёГ№Өі§УҰҪЁЙиЙъІъПЯіөјд¶аЙЩёцЈҝК№өГЙМЖ·![]() өДФВАыИуОӘЧоҙуЈ®
өДФВАыИуОӘЧоҙуЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘЖҪГжЦұҪЗЧшұкПө![]() ЦРЈ¬ЗъПЯ
ЦРЈ¬ЗъПЯ![]() өД·ҪіМОӘ
өД·ҪіМОӘ![]() Ј¬ТФФӯөг
Ј¬ТФФӯөг![]() ОӘј«өгЈ¬
ОӘј«өгЈ¬![]() ЦбөДХэ°лЦбОӘј«ЦбҪЁБўј«ЧшұкПөЈ¬ЦұПЯ
ЦбөДХэ°лЦбОӘј«ЦбҪЁБўј«ЧшұкПөЈ¬ЦұПЯ![]() өДј«Чшұк·ҪіМОӘ
өДј«Чшұк·ҪіМОӘ![]() Ј®ИфҪ«ЗъПЯ
Ј®ИфҪ«ЗъПЯ![]() ЙПөДЛщУРөгөДәбЧшұкЛхРЎөҪФӯАҙөДТ»°лЈ¬ЧЭЧшұкЙміӨөҪФӯАҙөД
ЙПөДЛщУРөгөДәбЧшұкЛхРЎөҪФӯАҙөДТ»°лЈ¬ЧЭЧшұкЙміӨөҪФӯАҙөД![]() ұ¶Ј¬өГЗъПЯ
ұ¶Ј¬өГЗъПЯ![]() Ј®
Ј®
ЈЁ1Ј©РҙіцЦұПЯ![]() әНЗъПЯ
әНЗъПЯ![]() өДЦұҪЗЧшұк·ҪіМЈ»
өДЦұҪЗЧшұк·ҪіМЈ»
ЈЁ2Ј©Йиөг![]() Ј¬ ЦұПЯ
Ј¬ ЦұПЯ![]() УлЗъПЯ
УлЗъПЯ![]() өДБҪёцҪ»өг·ЦұрОӘ
өДБҪёцҪ»өг·ЦұрОӘ![]() Ј¬
Ј¬![]() Ј¬Зу
Ј¬Зу![]() өДЦөЈ®
өДЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝijѧУёЯЦРИэёцДкј¶№ІУР4000ИЛЈ¬ОӘБЛБЛҪвёчДкј¶С§ЦЬД©ФЪјТөДС§П°ЗйҝцЈ¬ПЦНЁ№э·ЦІгійСщөД·Ҫ·Ё»сөГПа№ШКэҫЭИзПВЈЁөҘО»ЈәРЎКұЈ©Ј¬ЖдЦРёЯТ»С§ЙъЦЬД©өДЖҪҫщС§П°КұјдјЗОӘ![]() .
.
ёЯТ»Јә14 15 15.5 16.5 17 17 18 19
ёЯ¶юЈә15 16 16 16 17 17 18.5
ёЯИэЈә16 17 18 21.5 24
(1)ЗуГҝёцДкј¶өДС§ЙъИЛКэЈ»
(2)ҙУёЯИэұ»ійІйөДН¬С§ЦРЛж»ъійИЎ2ИЛЈ¬Зу2ИЛС§П°Кұјдҫщі¬№э![]() өДёЕВК.
өДёЕВК.
Ійҝҙҙр°ёәНҪвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com