
【题目】[选修4-5:不等式选讲]
已知函数![]() (
(![]() ),若
),若![]() 的解集是
的解集是![]() .
.
(1)求![]() 的值;
的值;
(2)若关于![]() 的不等式
的不等式![]() 有解,求实数
有解,求实数![]() 的取值范围.
的取值范围.
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】在如图所示的圆锥中,OP是圆锥的高,AB是底面圆的直径,点C是弧AB的中点,E是线段AC的中点,D是线段PB的中点,且PO=2,OB=1. 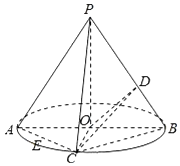
(1)试在PB上确定一点F,使得EF∥面COD,并说明理由;
(2)求点A到面COD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先后随机投掷2枚正方体骰子,其中x表示第1枚骰子出现的点数,y表示第2枚骰子出现的点数,
(1)求点P(x,y)在直线y=x﹣1上的概率;
(2)求点P(x,y)满足y2<4x的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知,圆C:x2+y2﹣8y+12=0,直线l:ax+y+2a=0.
(1)当a为何值时,直线l与圆C相切;
(2)当直线l与圆C相交于A、B两点,且AB=2 ![]() 时,求直线l的方程.
时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C1: ![]() +
+ ![]() =1(a>b>0)过点A(1,
=1(a>b>0)过点A(1, ![]() ),其焦距为2.
),其焦距为2. 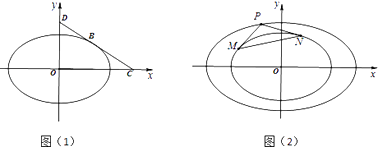
(1)求椭圆C1的方程;
(2)已知椭圆具有如下性质:若椭圆的方程为 ![]() +
+ ![]() =1(a>b>0),则椭圆在其上一点A(x0 , y0)处的切线方程为
=1(a>b>0),则椭圆在其上一点A(x0 , y0)处的切线方程为 ![]() +
+ ![]() =1,试运用该性质解决以下问题:
=1,试运用该性质解决以下问题:
(i)如图(1),点B为C1在第一象限中的任意一点,过B作C1的切线l,l分别与x轴和y轴的正半轴交于C,D两点,求△OCD面积的最小值;
(ii)如图(2),过椭圆C2: ![]() +
+ ![]() =1上任意一点P作C1的两条切线PM和PN,切点分别为M,N.当点P在椭圆C2上运动时,是否存在定圆恒与直线MN相切?若存在,求出圆的方程;若不存在,请说明理由.
=1上任意一点P作C1的两条切线PM和PN,切点分别为M,N.当点P在椭圆C2上运动时,是否存在定圆恒与直线MN相切?若存在,求出圆的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)(ω>0,|φ|< ![]() ),其图象相邻两条对称轴之间的距离为
),其图象相邻两条对称轴之间的距离为 ![]() ,且函数f(x+
,且函数f(x+ ![]() )是偶函数,下列判断正确的是( )
)是偶函数,下列判断正确的是( )
A.函数f(x)的最小正周期为2π
B.函数f(x)的图象关于点( ![]() ,0)d对称
,0)d对称
C.函数f(x)的图象关于直线x=﹣ ![]() 对称
对称
D.函数f(x)在[ ![]() ,π]上单调递增
,π]上单调递增
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等差数列{an}中,已知an>0,a1+a2+a3=15,且a1+2,a2+5,a3+13构成等比数列{bn}的前三项.
(1)求数列{an},{bn}的通项公式;
(2)求数列{anbn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂家为了了解某新产品使用者的年龄情况,现随机调査100 位使用者的年龄整理后画出的频率分布直方图如图所示.

(1)求100名使用者中各年龄组的人数,并利用所给的频率分布直方图估计所有使用者的平均年龄;
(2)若已从年龄在![]() 的使用者中利用分层抽样选取了6人,再从这6人中选出2人,求这2人在不同的年龄组的概率.
的使用者中利用分层抽样选取了6人,再从这6人中选出2人,求这2人在不同的年龄组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥S一ABCD中,已知AD∥BC,∠ADC=90°,∠BAD=135°,AD=DC= ![]() ,SA=SC=SD=2.
,SA=SC=SD=2.
(I)求证:AC⊥SD;
(Ⅱ)求二面角A﹣SB﹣C的余弦值.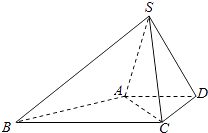
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com