
分析 (1)利用(a+b+c)2=a2+b2+c2+2ab+2bc+2ac=1,利用重要不等式,通过放缩证明即可.
(2)利用分析法由$\sqrt{\frac{{a}^{2}+{b}^{2}+{c}^{2}}{3}}$≥$\frac{a+b+c}{3}$,得到条件(a-b)2+(b-c)2+(c-a)2≥0,
推出结论.
解答 证明:(1)∵a+b+c=1,
∴(a+b+c)2=a2+b2+c2+2ab+2bc+2ac=1,
∵2ab≤a2+b2,2bc≤c2+b2,2ac≤a2+c2,
∴a2+b2+c2+2ab+2bc+2ac=1≤3(a2+b2+c2),
∴a2+b2+c2≥$\frac{1}{3}$.(7分)
(2)由已知得a+b+c>0,
欲证$\sqrt{\frac{{a}^{2}+{b}^{2}+{c}^{2}}{3}}$≥$\frac{a+b+c}{3}$,只需证$\frac{{a}^{2}+{b}^{2}+{c}^{2}}{3}$≥$\frac{(a+b+c)^{2}}{9}$,
只需证3(a2+b2+c2)≥(a+b+c)2,
只需证2a2+2b2+2c2-2ab-2bc-2ac≥0,
即证(a-b)2+(b-c)2+(c-a)2≥0,
上述不等式显然成立,故原不等式成立.(14分)
点评 本题考查不等式的证明,考查分析法以及综合法的应用,考查逻辑推理能力.


科目:高中数学 来源: 题型:选择题
| A. | x${\;}^{2}+\frac{{y}^{2}}{3}$=1 | B. | $\frac{{x}^{2}}{16}-\frac{{y}^{2}}{48}$=1 | C. | $\frac{{x}^{2}}{2}-\frac{{y}^{2}}{6}$=1 | D. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. |  | C. | 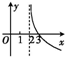 | D. | 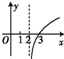 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com