
【题目】某种“笼具”由内,外两层组成,无下底面,内层和外层分别是一个圆锥和圆柱,其中圆柱与圆锥的底面周长相等,圆柱有上底面,制作时需要将圆锥的顶端剪去,剪去部分和接头忽略不计,已知圆柱的底面周长为![]() ,高为
,高为![]() ,圆锥的母线长为
,圆锥的母线长为![]() .
.
(1)求这种“笼具”的体积;
(2)现要使用一种纱网材料制作50个“笼具”,该材料的造价为每平方米8元,共需多少元?

 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的短轴长为2,且函数
的短轴长为2,且函数![]() 的图象与椭圆
的图象与椭圆![]() 仅有两个公共点,过原点的直线
仅有两个公共点,过原点的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点.
两点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)点![]() 为线段
为线段![]() 的中垂线与椭圆
的中垂线与椭圆![]() 的一个公共点,求
的一个公共点,求![]() 面积的最小值,并求此时直线
面积的最小值,并求此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
: ![]() ,定点
,定点![]() (常数
(常数![]() )的直线
)的直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 、
、![]() 两点.
两点.
(1)若点![]() 的坐标为
的坐标为![]() ,求证:
,求证: ![]()
(2)若![]() ,以
,以![]() 为直径的圆的位置是否恒过一定点?若存在,求出这个定点,若不存在,请说明理由.
为直径的圆的位置是否恒过一定点?若存在,求出这个定点,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2016-2017学年辽宁省六校协作体高二下学期期初数学(理)】已知圆![]() 的圆心在坐标原点,且与直线
的圆心在坐标原点,且与直线![]() 相切.
相切.
(1)求直线![]() 被圆
被圆![]() 所截得的弦
所截得的弦![]() 的长;
的长;
(2)过点![]() 作两条与圆
作两条与圆![]() 相切的直线,切点分别为
相切的直线,切点分别为![]() 求直线
求直线![]() 的方程;
的方程;
(3)若与直线![]() 垂直的直线
垂直的直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() ,若
,若![]() 为钝角,求直线
为钝角,求直线![]() 在
在![]() 轴上的截距的取值范围.
轴上的截距的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2013江苏,理17】如图,在平面直角坐标系xOy中,点A(0,3),直线l:y=2x-4.设圆C的半径为1,圆心在l上.
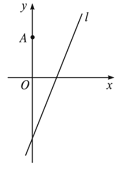
(1)若圆心C也在直线y=x-1上,过点A作圆C的切线,求切线的方程;
(2)若圆C上存在点M,使MA=2MO,求圆心C的横坐标a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的图象一个最高点为P(
)的图象一个最高点为P( ![]() ,2),相邻最低点为Q(
,2),相邻最低点为Q( ![]() ,﹣2),当x∈[﹣
,﹣2),当x∈[﹣ ![]() ,
, ![]() ]时,求f(x)的值域.
]时,求f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD,PD⊥底面ABCD,且底面ABCD是边长为2的正方形,M、N分别为PB、PC的中点. 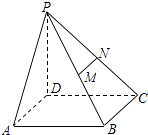
(1)证明:MN∥平面PAD;
(2)若PA与平面ABCD所成的角为45°,求四棱锥P﹣ABCD的体积V.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(sinx,1),
=(sinx,1), ![]() =
= ![]() ,函数f(x)=
,函数f(x)= ![]() 的最大值为6.
的最大值为6.
(1)求A;
(2)将函数f(x)的图象向左平移 ![]() 个单位,再将所得图象上各点的横坐标缩短为原来的
个单位,再将所得图象上各点的横坐标缩短为原来的 ![]() 倍,纵坐标不变,得到函数y=g(x)的图象.求g(x)在[0,
倍,纵坐标不变,得到函数y=g(x)的图象.求g(x)在[0, ![]() ]上的值域.
]上的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com