
分析 由(m-1)(a-1)>0得到a、m的范围,结合对数式有意义判断①;直接求出双曲线的渐近线方程判断②;由线性回归方程中预报变量与变量x的关系判断③;求出正态分布的概率判断④.
解答 解:由(m-1)(a-1)>0,解得$\left\{\begin{array}{l}{m>1}\\{a>1}\end{array}\right.$或$\left\{\begin{array}{l}{m<1}\\{a<1}\end{array}\right.$,但是$\left\{\begin{array}{l}{m<0}\\{a<0}\end{array}\right.$时,logam无意义,利用对数函数的单调性可得(m-1)(a-1)>0是logam>0的必要不充分条件,①正确;
由$\frac{y^2}{2}$-x2=1,得$a=\sqrt{2}$,b=1,∴其渐近线方程为$y=±\frac{a}{b}x$=±$\sqrt{2}$x,②正确;
线性回归方程为$\widehat{y}$=3+2x,当变量x增加2个单位,其预报值平均增加$\widehat{{y}_{△}}$=(3+2(x+2))-(3+2x)=4个单位,③正确;
随机变量ξ服从正态分布N(0,1),若P(ξ>1)=0.2,则P(-1<ξ<0)=0.3,④错误.
∴正确命题的序号为①②③.
故答案为:①②③.
点评 本题考查命题的真假判断与运用,考查充分必要条件的判定方法,考查了正态分布概率的求法,是基础题.


 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-3)∪(0,3) | B. | (-3,0)∪(0,3) | C. | (-∞,-3)∪(3,+∞) | D. | (-3,0)∪(3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
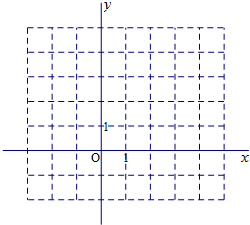 已知不等式组$\left\{{\begin{array}{l}{3x-y-3≥0}\\{x-2y-1≤0}\\{2x+y-7≤0}\end{array}}\right.$表示的区域为D,
已知不等式组$\left\{{\begin{array}{l}{3x-y-3≥0}\\{x-2y-1≤0}\\{2x+y-7≤0}\end{array}}\right.$表示的区域为D,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | d<0 | B. | S11>0 | ||
| C. | {Sn}中的最大项为S11 | D. | |a6|>|a7| |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\sqrt{3}$ | C. | -$\sqrt{3}$ | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com