
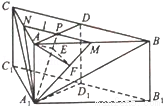
(12分)如图,在三棱柱ABC﹣A1B1C1中,侧棱AA1⊥底面ABC,AB=AC=2AA1,∠BAC=120°,D,D1分别是线段BC,B1C1的中点,P是线段AD的中点.
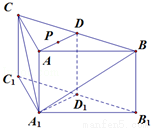
(I)在平面ABC内,试做出过点P与平面A1BC平行的直线l,说明理由,并证明直线l⊥平面ADD1A1;
(II)设(I)中的直线l交AB于点M,交AC于点N,求二面角A﹣A1M﹣N的余弦值.
(I)见解析(II)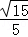
【解析】(I)在平面ABC内,过点P作直线l∥BC
∵直线l⊄平面A1BC,BC⊂平面A1BC,
∴直线l∥平面A1BC,
∵△ABC中,AB=AC,D是BC的中点,
∴AD⊥BC,结合l∥BC得AD⊥l
∵AA1⊥平面ABC,l⊂平面ABC,∴AA1⊥l
∵AD、AA1是平面ADD1A1内的相交直线
∴直线l⊥平面ADD1A1;
(II)连接A1P,过点A作AE⊥A1P于E,过E点作EF⊥A1M于F,连接AF
由(I)知MN⊥平面A1AE,结合MN⊂平面A1MN得平面A1MN⊥平面A1AE,
∵平面A1MN∩平面A1AE=A1P,AE⊥A1P,∴AE⊥平面A1MN,
∵EF⊥A1M,EF是AF在平面A1MN内的射影,
∴AF⊥A1M,可得∠AFE就是二面角A﹣A1M﹣N的平面角
设AA1=1,则由AB=AC=2AA1,∠BAC=120°,可得∠BAD=60°,AB=2且AD=1
又∵P为AD的中点,∴M是AB的中点,得AP=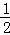 ,AM=1
,AM=1
Rt△A1AP中,A1P= =
=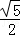 ;Rt△A1AM中,A1M=
;Rt△A1AM中,A1M=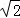
∴AE= =
= ,AF=
,AF=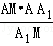 =
=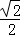
∴Rt△AEF中,sin∠AFE=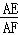 =
= ,可得cos∠AFE=
,可得cos∠AFE=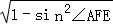 =
=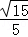
即二面角A﹣A1M﹣N的余弦值等于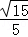 .
.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
 如图,在三棱柱ABC-A'B'C'中,若E、F分别为AB、AC的中点,平面EB'C'F将三棱柱分成体积为V1、V2的两部分,那么V1:V2为( )
如图,在三棱柱ABC-A'B'C'中,若E、F分别为AB、AC的中点,平面EB'C'F将三棱柱分成体积为V1、V2的两部分,那么V1:V2为( )| A、3:2 | B、7:5 | C、8:5 | D、9:5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=60°,四边形BCC1B1为矩形,若AB⊥BC且AB=4,BC=3
如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=60°,四边形BCC1B1为矩形,若AB⊥BC且AB=4,BC=3查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•通州区一模)如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=2,AB=2
(2013•通州区一模)如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=2,AB=2| 2 |
| AN |
| AB |
| CM |
| CC1 |
| 5 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在三棱柱ABC-A1B1C1中,AA1⊥面ABC,AC⊥BC,E分别在线段B1C1上,B1E=3EC1,AC=BC=CC1=4.
如图,在三棱柱ABC-A1B1C1中,AA1⊥面ABC,AC⊥BC,E分别在线段B1C1上,B1E=3EC1,AC=BC=CC1=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com