Question

【题目】某食品厂为了检查一条自动包装流水线的生产情况，随机抽取该流水线上的件产品作为样本，称出它们的重量（单位：克），重量的分组区间为，，…，，由此得到样本的频率分布方图，如图所示.

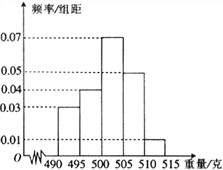
（1）在上述抽取的件产品中任取件，设为取到重量超过克的产品件数，求的概率；

（2）从上述件产品中任取件，设为取到重量超过克的产品件数，求的分布列与期望.

Answer 1

【答案】(1)；(2)答案见解析.

【解析】分析：(1）由频率分布直方图近似可得重量超过克的产品件数为6，结合古典概型计算公式可得满足题意的概率值为.

(2）的所有可能取值为，，，由(1）知重量超过克的产品有件，则，，，据此可得分布列，结合分布列计算期望可得.

详解：(1）由频率分布直方图可知，重量超过克的产品件数是：

，

所以.

(2）的所有可能取值为，，，由(1）知重量超过克的产品有件，

，

，

，

所以的分布列为：

	0	1	2

.