[题目]有以下命题:①如果向量与任何向量不能构成空间向量的一组基底.那么的关系是不共线,②为空间四点.且向量不构成空间的一个基底.那么点一定共面,③已知向量是空间的一个基底.则向量.也是空间的一个基底.其中正确的命题是( )A. ①②B. ①③C. ②③D. ①②③ 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】有以下命题：①如果向量与任何向量不能构成空间向量的一组基底，那么的关系是不共线；②为空间四点，且向量不构成空间的一个基底，那么点一定共面；③已知向量是空间的一个基底，则向量，也是空间的一个基底。其中正确的命题是（）

A. ①②B. ①③C. ②③D. ①②③

【答案】C

【解析】

根据空间向量的基底判断②③的正误，找出反例判断①命题的正误，即可得到正确选项．

解：①如果向量与任何向量不能构成空间向量的一组基底，那么的关系是不共线；所以不正确．反例：如果有一个向量为零向量，共线但不能构成空间向量的一组基底，所以不正确．

②O，A，B，C为空间四点，且向量不构成空间的一个基底，那么点O，A，B，C一定共面；这是正确的．

③已知向量是空间的一个基底，则向量，也是空间的一个基底；因为三个向量非零不共线，正确．

故选：C．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】在棱长为1的正方体中，点是对角线上的动点（点与不重合），则下列结论正确的是__________

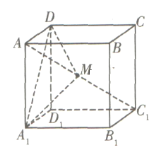
①存在点，使得平面平面；

②存在点，使得平面平面；

③的面积可能等于；

④若分别是在平面与平面的正投影的面积，则存在点，使得

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，在直角坐标系xOy中，圆O：x2+y2=4与x轴负半轴交于点A，过点A的直线AM，AN分别与圆O交于M，N两点，设直线AM、AN的斜率分别为k1、k2．

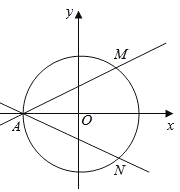
（1）若，求△AMN的面积；

（2）若k1k2=-2，求证：直线MN过定点．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在直角坐标系xOy中，已知椭圆E的中心在原点，长轴长为8，椭圆在X轴上的两个焦点与短轴的一个顶点构成等边三角形．

求椭圆的标准方程；

过椭圆内一点的直线与椭圆E交于不同的A，B两点，交直线于点N，若，求证：为定值，并求出此定值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在正方体ABCD﹣A1B1C1D1中，当点E在B1D1（与B1，D1不重合）上运动时，总有：

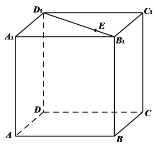
①AE∥BC1； ②平面AA1E⊥平面BB1D1D；

③AE∥平面BC1D； ④A1C⊥AE．

以上四个推断中正确的是（）

A.①②B.①④C.②④D.③④

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数．

（1）当时，求曲线在点处的切线方程；

（2）求函数的单调区间；

（3）当时，求函数在上区间零点的个数.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数．

（1）讨论的单调性并指出相应单调区间；

（2）若，设是函数的两个极值点，若，且恒成立，求实数k的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】为推动更多人阅读，联合国教科文组织确定每年的月日为“世界读书日”.设立目的是希望居住在世界各地的人，无论你是年老还是年轻，无论你是贫穷还是富裕，都能享受阅读的乐趣，都能尊重和感谢为人类文明做出过巨大贡献的思想大师们，都能保护知识产权.为了解不同年龄段居民的主要阅读方式，某校兴趣小组在全市随机调查了名居民，经统计这人中通过电子阅读与纸质阅读的人数之比为,将这人按年龄分组，其中统计通过电子阅读的居民得到的频率分布直方图如图所示.