
分析 (1)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;
(2)求出函数的导数,得到f′(2)=0,解出即可;
(3)通过讨论a的范围,求出函数f(x)的最小值,结合函数的图象,求出a的范围即可.
解答 解:(1)因为f(x)=x-alnx,所以$f'(x)=1-\frac{a}{x}=\frac{x-a}{x}$(x>0),
当a≤0时,f'(x)>0,所以f(x)的单调递增区间是(0,+∞);
当a>0时,若0<x<a,f'(x)<0;若x>a,f'(x)>0;
所以f(x)的单调递减区间是(0,a),单调递增区间是(a,+∞).
(2)因为当x=2时,函数f(x)取得极小值,所以f'(2)=0,即$1-\frac{a}{2}=0$,解得a=2.
(3)当a≤0时,f(x)的单调递增区间是(0,+∞),函数f(x)至多一个零点,不符合题意.
当a>0时,由(1)得f(x)的单调递减区间是(0,a),单调递增区间是(a,+∞),
所以f(x)min=f(a)=a(1-lna).
当x→0时,f(x)→+∞,所以函数f(x)的图象可知,f(a)=a(1-lna)<0,解得a>e,
所以a的取值范围是(e,+∞).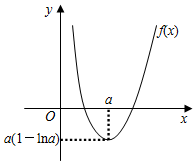
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,转化思想,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | y与x具有正的线性相关关系 | |
| B. | 若该大学某女生身高为170cm,则可断定其体重必为58.79kg | |
| C. | 过该大学某女生身高增加1cm,则其体重约增加0.85kg | |
| D. | 回归直线过样本的中心$(\overline x,\overline y)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
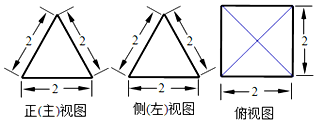
| A. | 16 | B. | 12 | C. | $\frac{4\sqrt{3}}{3}$+4 | D. | 4$\sqrt{3}$+4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 直角三角形 | C. | 等边三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
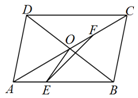 已知平行四边形ABCD中,$|\overrightarrow{AB}|=3$,$|\overrightarrow{AD}|=2$,对角线AC交BD于点O,AB上一点E满足$\overrightarrow{OE}•\overrightarrow{BD}=0$,F为AC上任意一点.
已知平行四边形ABCD中,$|\overrightarrow{AB}|=3$,$|\overrightarrow{AD}|=2$,对角线AC交BD于点O,AB上一点E满足$\overrightarrow{OE}•\overrightarrow{BD}=0$,F为AC上任意一点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 我国古代,9是数字之极,代表尊贵之意,所以中国古代皇家建筑中包含许多与9相关的设计.例如,北京天坛圆丘的地面由扇环形的石板铺成(如图所示),最高一层是一块天心石,围绕它的第一圈有9块石板,从第二圈开始,每一圈比前一圈多9块,共有9圈,则前9圈的石板总数是405.
我国古代,9是数字之极,代表尊贵之意,所以中国古代皇家建筑中包含许多与9相关的设计.例如,北京天坛圆丘的地面由扇环形的石板铺成(如图所示),最高一层是一块天心石,围绕它的第一圈有9块石板,从第二圈开始,每一圈比前一圈多9块,共有9圈,则前9圈的石板总数是405.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com