
【题目】过双曲线![]() 的左焦点
的左焦点![]() 作圆
作圆![]() 的切线交双曲线的右支于点
的切线交双曲线的右支于点![]() ,且切点为
,且切点为![]() ,已知
,已知![]() 为坐标原点,
为坐标原点,![]() 为线段
为线段![]() 的中点(
的中点(![]() 点在切点
点在切点![]() 的右侧),若
的右侧),若![]() 的周长为
的周长为![]() ,则双曲线的渐近线的方程为( )
,则双曲线的渐近线的方程为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
先从双曲线方程得:a,b.连OT,则OT⊥F1T,在直角三角形OTF1中,|F1T|=b.连PF2,M为线段F1P的中点,O为坐标原点得出|MO|﹣|MT|![]() PF2﹣(
PF2﹣( ![]() MF1﹣F1T)
MF1﹣F1T)![]() (PF2﹣MF1)﹣b最后结合周长与勾股定理可得结果.
(PF2﹣MF1)﹣b最后结合周长与勾股定理可得结果.
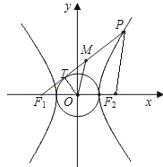
解:连OT,则OT⊥F1T,
在直角三角形OTF1中,|F1T|![]() b.
b.
连PF2,M为线段F1P的中点,O为坐标原点
∴OM![]() PF2,
PF2,
∴|MO|﹣|MT|![]() PF2﹣(
PF2﹣( ![]() PF1﹣F1T)
PF1﹣F1T)![]() (PF2﹣PF1)+b
(PF2﹣PF1)+b
![]() b﹣a.
b﹣a.
又|MO|+|MT|+|TO|=![]() ,即|MO|+|MT|=3a
,即|MO|+|MT|=3a
故|MO|=![]() , |MT|=
, |MT|=![]() ,
,
由勾股定理可得:![]() ,即
,即![]()
∴渐近线方程为:![]()
故选:B


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,从参加环保知识竞赛的1200名学生中抽出![]() 名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:
名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:

(1)![]() 这一组的频数、频率分别是多少?
这一组的频数、频率分别是多少?
(2)估计这次环保知识竞赛的及格率。(![]() 分及以上为及格)
分及以上为及格)
(3)若准备取成绩最好的300名发奖,则获奖的最低分数约为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点![]() 为圆
为圆![]() :
:![]() 上一动点,过点
上一动点,过点![]() 分别作
分别作![]() 轴,
轴,![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() ,
,![]() ,连接
,连接![]() 延长至点
延长至点![]() ,使得
,使得![]() ,点
,点![]() 的轨迹记为曲线
的轨迹记为曲线![]() .
.
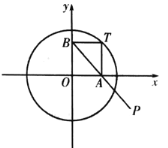
(1)求曲线![]() 的方程;
的方程;
(2)若点![]() ,
,![]() 分别位于
分别位于![]() 轴与
轴与![]() 轴的正半轴上,直线
轴的正半轴上,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,试问在曲线
两点,试问在曲线![]() 上是否存在点
上是否存在点![]() ,使得四边形
,使得四边形![]() 为平行四边形,若存在,求出直线
为平行四边形,若存在,求出直线![]() 方程;若不存在,说明理由.
方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】市面上有某品牌![]() 型和
型和![]() 型两种节能灯,假定
型两种节能灯,假定![]() 型节能灯使用寿命都超过5000小时,经销商对
型节能灯使用寿命都超过5000小时,经销商对![]() 型节能灯使用寿命进行了调查统计,得到如下频率分布直方图:
型节能灯使用寿命进行了调查统计,得到如下频率分布直方图:

某商家因原店面需要重新装修,需租赁一家新店面进行周转,合约期一年.新店面需安装该品牌节能灯5支(同种型号)即可正常营业.经了解,![]() 型20瓦和
型20瓦和![]() 型55瓦的两种节能灯照明效果相当,都适合安装.已知
型55瓦的两种节能灯照明效果相当,都适合安装.已知![]() 型和
型和![]() 型节能灯每支的价格分别为120元、25元,当地商业电价为0.75元/千瓦时.假定该店面一年周转期的照明时间为3600小时,若正常营业期间灯坏了立即购买同型灯管更换.(用频率估计概率)
型节能灯每支的价格分别为120元、25元,当地商业电价为0.75元/千瓦时.假定该店面一年周转期的照明时间为3600小时,若正常营业期间灯坏了立即购买同型灯管更换.(用频率估计概率)
(Ⅰ)根据频率直方图估算![]() 型节能灯的平均使用寿命;
型节能灯的平均使用寿命;
(Ⅱ)根据统计知识知,若一支灯管一年内需要更换的概率为![]() ,那么
,那么![]() 支灯管估计需要更换
支灯管估计需要更换![]() 支.若该商家新店面全部安装了
支.若该商家新店面全部安装了![]() 型节能灯,试估计一年内需更换的支数;
型节能灯,试估计一年内需更换的支数;
(Ⅲ)若只考虑灯的成本和消耗电费,你认为该商家应选择哪种型号的节能灯,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
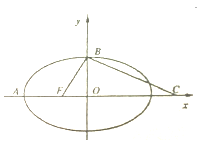
【题目】如图,F是椭圆![]() 的左焦点,椭圆的离心率为
的左焦点,椭圆的离心率为![]() ,B为椭圆的左顶点和上顶点,点C在x轴上,
,B为椭圆的左顶点和上顶点,点C在x轴上,![]() ,
,![]() 的外接圆M恰好与直线
的外接圆M恰好与直线![]() :
:![]() 相切.
相切.
![]() 1
1![]() 求椭圆的方程;
求椭圆的方程;
![]() 2
2![]() 过点C的直线
过点C的直线![]() 与已知椭圆交于P,Q两点,且
与已知椭圆交于P,Q两点,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为![]() 的正方体
的正方体![]() 中,
中,![]() ,
,![]() ,
,![]() 分别是棱
分别是棱![]() 、
、![]() 和
和![]() 所在直线上的动点:
所在直线上的动点:

(1)求![]() 的取值范围:
的取值范围:
(2)若![]() 为面
为面![]() 内的一点,且
内的一点,且![]() ,
,![]() ,求
,求![]() 的余弦值:
的余弦值:
(3)若![]() 、
、![]() 分别是所在正方形棱的中点,试问在棱
分别是所在正方形棱的中点,试问在棱![]() 上能否找到一点
上能否找到一点![]() ,使
,使![]() 平面
平面![]() ?若能,试确定点
?若能,试确定点![]() 的位置,若不能,请说明理由.
的位置,若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国西部某省![]() 级风景区内住着一个少数民族村,该村投资了
级风景区内住着一个少数民族村,该村投资了![]() 万元修复和加强民俗文化基础设施,据调查,修复好村民俗文化基础设施后,任何一个月内(每月按
万元修复和加强民俗文化基础设施,据调查,修复好村民俗文化基础设施后,任何一个月内(每月按![]() 天计算)每天的旅游人数
天计算)每天的旅游人数![]() 与第
与第![]() 天近似地满足
天近似地满足![]() (千人),且参观民俗文化村的游客人均消费
(千人),且参观民俗文化村的游客人均消费![]() 近似地满足
近似地满足![]() (元).
(元).
(1)求该村的第x天的旅游收入![]() ,并求最低日收入为多少?(单位:千元,
,并求最低日收入为多少?(单位:千元,![]() ,
,![]() );
);
(2)若以最低日收入的![]() 作为每一天的纯收入计量依据,并以纯收入的
作为每一天的纯收入计量依据,并以纯收入的![]() 税率收回投资成本,试问该村在两年内能否收回全部投资成本?
税率收回投资成本,试问该村在两年内能否收回全部投资成本?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com