【题目】有4个不同的球，4个不同的盒子，把球全部放入盒子内.
（1）共有几种放法？
（2）恰有2个盒子不放球，有几种放法？
【答案】（1）256种（2）84种
【解析】
（1）明确共有4个球，每个球都有4种放法，盒子可以不放球，根据分步计数原理求解.
（2）首先明确有两个盒子不放球的含义是将4个球放入2个盒子中，放球分为两类，一类是1个盒子放3个另一个放1个，二类是两个盒子各放2个，分别求出每一类的放法，再用加法计数原理求解.
（1）每一个球有4种放法，故共有44＝256（种）
（2）恰有2个盒子不放球，也就是把4个不同的小球只放入2个盒子中，有两类放法；
第一类，1个盒子放3个小球，1个盒子放1个小球，先把小球分组，有
种，再放到2个小盒中有
种放法，共有
种方法；
第二类，2个盒子中各放2个小球有
种放法，
故恰有2个盒子不放球的方法共有
种放法.
阅读快车系列答案科目：高中数学 来源： 题型：
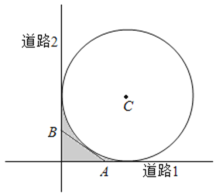
【题目】如图，某城市有一块半径为
（单位：百米）的圆形景观，圆心为
，有两条与圆形景观相切且互相垂直的道路.最初规划在拐角处
图中阴影部分
只有一块绿化地，后来有众多市民建议在绿化地上建一条小路，便于市民快捷地往返两条道路.规划部门采纳了此建议，决定在绿化地中增建一条与圆相切的小道
问：
两点应选在何处可使得小道
最短？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，已知四棱锥S－ABCD的底面ABCD是正方形，SA⊥底面ABCD，E是SC上的一点.
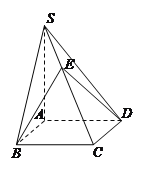
(1)求证：平面EBD⊥平面SAC；
(2)设SA＝4，AB＝2，求点A到平面SBD的距离；
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】关于
的说法，错误的是（ ）
A.展开式中的二项式系数之和为1024
B.展开式中第6项的二项式系数最大
C.展开式中第5项和第7项的二项式系数最大
D.展开式中第6项的系数最小
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在四棱锥PABCD中，AD∥BC，平面PAC⊥平面ABCD，AB=AD=DC=1，
∠ABC=∠DCB=60，E是PC上一点.
（Ⅰ）证明：平面EAB⊥平面PAC；
（Ⅱ）若△PAC是正三角形，且E是PC中点，求三棱锥AEBC的体积.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】研究表明某地的山高
(
)与该山的年平均气温
(
)具有相关关系，根据所采集的数据得到线性回归方程
，则下列说法错误的是（ ）
A.年平均气温为
时该山高估计为
B.该山高为
处的年平均气温估计为
C.该地的山高与该山的年平均气温的正负相关性与回归直线的斜率的估计值有关
D.该地的山高与该山的年平均气温成负相关关系
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆C：
过点
，且离心率为
（Ⅰ）求椭圆C的方程；
（Ⅱ）若过原点的直线
与椭圆C交于P、Q两点，且在直线
上存在点M，使得
为等边三角形，求直线的方程。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某工厂预购软件服务，有如下两种方案：
方案一：软件服务公司每日收取工厂60元，对于提供的软件服务每次10元；
方案二：软件服务公司每日收取工厂200元，若每日软件服务不超过15次，不另外收费，若超过15次，超过部分的软件服务每次收费标准为20元.
（1）设日收费为
元，每天软件服务的次数为
，试写出两种方案中与的函数关系式；
（2）该工厂对过去100天的软件服务的次数进行了统计，得到如图所示的条形图，依据该统计数据，把频率视为概率，从节约成本的角度考虑，从两个方案中选择一个，哪个方案更合适？请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
