已知
的周长为
，面积为
，则的内切圆半径为
．将此结论类比到空间，已知四面体
的表面积为，体积为
，则四面体的内切球的半径
．
阅读快车系列答案科目：高中数学 来源： 题型：填空题
（5分）（2011•陕西）观察下列等式
1=1
2+3+4=9
3+4+5+6+7=25
4+5+6+7+8+9+10=49
照此规律，第五个等式应为 ．
查看答案和解析>>
科目：高中数学 来源： 题型：填空题
如图.小正六边形沿着大正六边形的边按顺时针方向滚动，小正六边形的边长是大正六边形的边长的一半.如果小正六边形沿着大正六边形的边滚动一周后返回出发时的位置，在这个过程中，向量
围绕着点
旋转了
角，其中为小正六边形的中心，则
.
查看答案和解析>>
科目：高中数学 来源： 题型：填空题
若三角形内切圆的半径为r，三边长为
，则三角形的面积
，根据类比思想，若四面体内切球半径为R，四个面的面积为S1、S2、S3、S4，则四面体的体积V= .
查看答案和解析>>
科目：高中数学 来源： 题型：填空题
将长度为
的线段分成
段，每段长度均为正整数，并要求这
段中的任意三段都不能构成三角形．例如，当
时，只可以分为长度分别为1,1,2的三段，此时的最大值为3；当
时，可以分为长度分别为1,2,4的三段或长度分别为1,1,2,3的四段，此时的最大值为4．则：
（1）当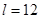
时，的最大值为________；（2）当
时，的最大值为________．
查看答案和解析>>
科目：高中数学 来源： 题型：填空题
凸函数的性质定理为：如果函数f(x)在区间D上是凸函数，则对于区间D内的任意x1，x2，…，xn，有
≤f(
)，已知函数y＝sinx在区间(0，π)上是凸函数，则在△ABC中，sinA＋sinB＋sinC的最大值为________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
求出
求出
，当
时，观察下列等式：
_______.
个等式为 ．
＝1，若以a、b、c为三边构造三角形，则c的取值范围是________．