
 如图所示,曲线段OMB是函数f(x)=x2(0<x<6)的图象,BA⊥x轴于A,曲线段OMB上一点M(t,f(t))处的切线PQ交x轴于P,交线段AB于Q,
如图所示,曲线段OMB是函数f(x)=x2(0<x<6)的图象,BA⊥x轴于A,曲线段OMB上一点M(t,f(t))处的切线PQ交x轴于P,交线段AB于Q,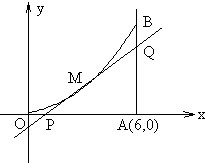 解:(Ⅰ)设点M(t,t2),又f'(x)=2x,
解:(Ⅰ)设点M(t,t2),又f'(x)=2x,| t |
| 2 |
| t |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| t3 |
| 4 |
| t3 |
| 4 |
| 3t2 |
| 4 |


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:
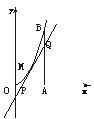 如图所示,曲线段OMB是函数f(x)=x2(0<x<6)的图象,BA⊥x轴于A,曲线段OMB上一点M(t,f(t))处的切线PQ交x轴于P,交线段AB于Q,
如图所示,曲线段OMB是函数f(x)=x2(0<x<6)的图象,BA⊥x轴于A,曲线段OMB上一点M(t,f(t))处的切线PQ交x轴于P,交线段AB于Q,查看答案和解析>>
科目:高中数学 来源: 题型:
(1)试用t表示切线PQ的方程;
(2)试用t表示△QAP的面积g(t),若函数g(t)在(m,n)上单调递减,试求出m的最小值;
(3)若S△QAP∈[![]() ,64],试求出点P横坐标的取值范围.
,64],试求出点P横坐标的取值范围.

查看答案和解析>>
科目:高中数学 来源: 题型:
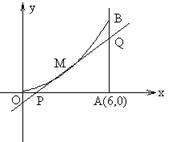
如图所示,曲线段OMB是函数f(x)=x2(0<x<6=的图象,BA⊥x轴于A,曲线段OMB上一点M(t,f(t))处的切线PQ交x轴于P,交线段AB于Q,⑴试用t表示切线PQ的方程;⑵试用t表示出△QAP的面积g(t);若函数g(t)在(m,n)上单调递减,试求出m的最小值;⑶若S△QAP∈[![]() ],试求出点P横坐标的取值范围
],试求出点P横坐标的取值范围
查看答案和解析>>
科目:高中数学 来源:2006年高考第一轮复习数学:14.5 导数的综合问题(解析版) 题型:解答题
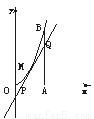
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com