
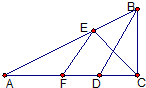
 如图,已知△ABC,BC=9cm,现有两个质点甲、乙同时从C点出发,甲沿路线C→B→A以每秒2cm的速度匀速向前移动,乙沿路线C→A以每秒1cm的速度匀速向前移动,当甲到达B点时,乙到达D点,并满足
如图,已知△ABC,BC=9cm,现有两个质点甲、乙同时从C点出发,甲沿路线C→B→A以每秒2cm的速度匀速向前移动,乙沿路线C→A以每秒1cm的速度匀速向前移动,当甲到达B点时,乙到达D点,并满足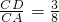 ,最后它们同时到达A点.
,最后它们同时到达A点.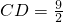 ,则AC=12,
,则AC=12,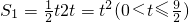 ,-----(10分)
,-----(10分)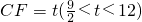 ,
,
 ,
,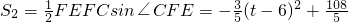 ,
,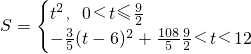 ----(16分)
----(16分)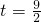 时有最大值
时有最大值 ;当t=6时有最大值
;当t=6时有最大值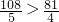 ,
,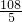 .--(18分)
.--(18分)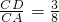 ,最后它们同时到达A点.可能CB+CA=2AC,CB:AB=CD:CA=3:8,进而求出AC,AB边的长,由余弦定理(或勾股定理)即可判断△ABC的形状;
,最后它们同时到达A点.可能CB+CA=2AC,CB:AB=CD:CA=3:8,进而求出AC,AB边的长,由余弦定理(或勾股定理)即可判断△ABC的形状;

科目:高中数学 来源: 题型:
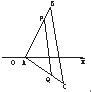 如图,已知△ABC的顶点坐标依次为A(1,0),B(5,8),C(7,-4),在边AB上有一点P,其横坐标为4,在AC上求一点Q,使线段PQ把△ABC分成面积相等的两部分.
如图,已知△ABC的顶点坐标依次为A(1,0),B(5,8),C(7,-4),在边AB上有一点P,其横坐标为4,在AC上求一点Q,使线段PQ把△ABC分成面积相等的两部分.查看答案和解析>>
科目:高中数学 来源: 题型:
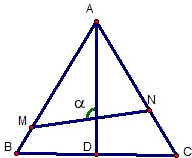 如图,已知△ABC是边长为1的正三角形,M、N分别是边AB、AC上的点,线段MN经过△ABC的中心G,设?MGA=a(
如图,已知△ABC是边长为1的正三角形,M、N分别是边AB、AC上的点,线段MN经过△ABC的中心G,设?MGA=a(| π |
| 3 |
| 2π |
| 3 |
| 1 |
| S12 |
| 1 |
| S22 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com