
| A. | $f(x)=\sqrt{{{(x-1)}^2}}$;g(x)=x-1 | B. | $f(x)=\frac{{{x^2}-1}}{x-1}$;g(x)=x+1 | ||
| C. | f(x)=lg(x+1)+lg(x-1);g(x)=lg(x2-1) | D. | f(x)=ex+1.ex-1;g(x)=e2x |
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
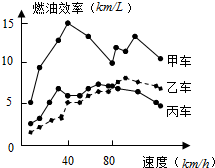 汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,如图描述了甲、乙、丙三两汽车在不同速度下的燃油效率情况.某城市机动车最高限速80千米/小时,相同条件下,用甲、乙、丙三两汽车在该市行驶,最省油是( )
汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,如图描述了甲、乙、丙三两汽车在不同速度下的燃油效率情况.某城市机动车最高限速80千米/小时,相同条件下,用甲、乙、丙三两汽车在该市行驶,最省油是( )| A. | 甲车 | B. | 乙车 | C. | 丙车 | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,2] | B. | [-1,2) | C. | [0,3) | D. | [0,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(1,{2015^{\frac{1}{2015}}}]$ | B. | $(0,{2015^{\frac{1}{2015}}}]$ | C. | $(1,{2015^{\frac{1}{2015}}})$ | D. | $(0,{2015^{\frac{1}{2015}}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
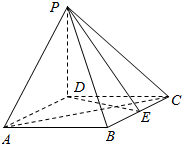 如图,四棱锥P-ABCD的底面ABCD为菱形,PD⊥底面ABCD,AD=2,∠DAB=60°,E为BC的中点.
如图,四棱锥P-ABCD的底面ABCD为菱形,PD⊥底面ABCD,AD=2,∠DAB=60°,E为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
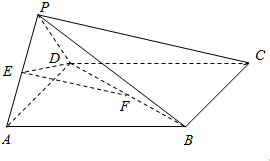 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,侧面PAD⊥底面ABCD,E,F分别为PA,BD的中点,PA=PD=AD=2,$AB=2\sqrt{2}$,∠DAB=45°.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,侧面PAD⊥底面ABCD,E,F分别为PA,BD的中点,PA=PD=AD=2,$AB=2\sqrt{2}$,∠DAB=45°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com