
【题目】设函数f(x)![]() .
.
(1)若x=1是函数f(x)的一个极值点,求k的值及f(x)单调区间;
(2)设g(x)=(x+1)ln(x+1)+f(x),若g(x)在[0,+∞)上是单调增函数,求实数k的取值范围;
(3)证明:当p>0,q>0及m<n(m,n∈N*)时,![]()
![]() .
.
【答案】(1)k=2,f(x)在(﹣∞,![]() )递增,在(
)递增,在(![]() ,1)递减,在(1,+∞)递增(2)k
,1)递减,在(1,+∞)递增(2)k![]() (3)证明见解析;
(3)证明见解析;
【解析】
(1)求出函数![]() 的导数,利用
的导数,利用![]() 求出k,令
求出k,令![]() 即求出函数的单调区间;
即求出函数的单调区间;
(2)求出函数![]() 的导数,问题转化为g′(x)=h(x)=ln(x+1)+kx2﹣x≥0恒成立,求出h(x)的导数,通过讨论k的范围,求出函数h(x)的最小值,求出k的范围即可;
的导数,问题转化为g′(x)=h(x)=ln(x+1)+kx2﹣x≥0恒成立,求出h(x)的导数,通过讨论k的范围,求出函数h(x)的最小值,求出k的范围即可;
(3)问题转化为证明![]() ln[1
ln[1 ]
]![]() ln[1
ln[1 ],不妨设p>q>0,构造函数φ(x)
],不妨设p>q>0,构造函数φ(x)![]() ln(1+ax),(x>0),其中a
ln(1+ax),(x>0),其中a![]() ∈(0,1),根据函数的单调性证明即可.
∈(0,1),根据函数的单调性证明即可.
解:(1)f′(x)=kx2﹣x﹣1,
∵x=1是函数f(x)的一个极值点,
∴f′(1)=k﹣1﹣1=0,解得:k=2,
∴f′(x)=2x2﹣x﹣1,
当f′(x)>0,即x![]() 或x>1时,f(x)递增,
或x>1时,f(x)递增,
当f′(x)<0,即![]() x<1时,f(x)递减,
x<1时,f(x)递减,
∴f(x)在(﹣∞,![]() )递增,在(
)递增,在(![]() ,1)递减,在(1,+∞)递增;
,1)递减,在(1,+∞)递增;
(2)g(x)=(x+1)ln(x+1)![]() x3
x3![]() x2﹣x,
x2﹣x,
g′(x)=ln(x+1)+kx2﹣x,
若g(x)在[0,+∞)上是单调增函数,则g′(x)≥0对x∈[0,+∞)恒成立,
令h(x)=ln(x+1)+kx2﹣x,h′(x)![]() 2kx﹣1
2kx﹣1![]() ,
,
(i)若k≤0,则h′(x)<0,h(x)在[0,+∞)递减,
∴h(x)≤h(0)=0,不合题意;
(ii)若k>0,由h′(x)=0解得:x=0,x![]() 1,
1,
①当0<k![]() 时,
时,![]() 0,
0,
∴x∈(0,![]() )时,h′(x)<0,h(x)递减,
)时,h′(x)<0,h(x)递减,
∴h(x)≤h(0)=0,不合题意;
②当k![]() 时,
时,![]() 0,
0,
∴x∈[0,+∞)时,h′(x)>0,h(x)递增,
∴h(x)≥h(0)=0,即g′(x)≥0对任意x∈[0,+∞)恒成立,
综上,k![]() 时,g(x)在[0,+∞)是单调递增函数;
时,g(x)在[0,+∞)是单调递增函数;
(3)∵![]()

 1
1 ,
,
∴![]()
![]()
[1]2n﹣1>[1
 ]2m﹣1,
]2m﹣1,

![]() ln[1
ln[1 ]
]![]() ln[1
ln[1 ],
],
不妨设p>q>0,则0![]() 1,
1,
构造函数φ(x)![]() ln(1+ax),(x>0),其中a
ln(1+ax),(x>0),其中a![]() ∈(0,1),
∈(0,1),
φ′(x) ,
,
由(2)知ln(x+1)>x![]() x2,
x2,
∴ln(ax+1)>ax![]() a2x,
a2x,
∴φ′(x) ,
,
∵a∈(0,1),x>0,
∴lna<0,ax>a2x![]() a2x,
a2x,
∴φ′(x)<0,φ(x)在(0,+∞)递减,
∵1≤m<n,∴0<2m﹣1<2n﹣1,
∴![]() ln[1
ln[1 ]
]![]() ln[1
ln[1 ],
],
故原不等式成立.


科目:高中数学 来源: 题型:
【题目】某医院体检中心为回馈大众,推出优惠活动:对首次参加体检的人员,按200元/次收费,并注册成为会员,对会员的后续体检给予相应优惠,标准如下:

该休检中心从所有会员中随机选取了100位对他们在本中心参加体检的次数进行统计,得到数据如表:

假设该体检中心为顾客体检一次的成本费用为150元,根据所给数据,解答下列问题:
(1)已知某顾客在此体检中心参加了3次体检,求这3次体检,该体检中心的平均利润;
(2)该体检中心要从这100人里至少体检3次的会员中,按体检次数用分层抽样的方法抽出5人,再从这5人中抽取2人,每人发放现金200元.用5表示体检3次的会员所得现金和,求![]() 的分布列及
的分布列及![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)(ω>0,|φ|![]() ),y=f(x)的图象关于直线x
),y=f(x)的图象关于直线x![]() 对称,且与x轴交点的横坐标构成一个公差为
对称,且与x轴交点的横坐标构成一个公差为![]() 的等差数列,则函数f(x)的导函数
的等差数列,则函数f(x)的导函数![]() 的一个单调减区间为( )
的一个单调减区间为( )
A.[![]() ,
,![]() ]B.[
]B.[![]() ,
,![]() ]C.[
]C.[![]() ,
,![]() ]D.[
]D.[![]() ,
,![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x-a|+|2x-1|(a∈R).
(1)当a=-1时,求f(x)≤2的解集;
(2)若f(x)≤|2x+1|的解集包含集合![]() ,求实数a的取值范围.
,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,半圆O的直径AB=2,点C在AB的延长线上,BC=1,点P为半圆上异于A,B两点的一个动点,以点P为直角顶点作等腰直角![]() ,且点D与圆心O分布在PC的两侧,设
,且点D与圆心O分布在PC的两侧,设![]() .
.
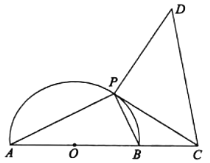
(1)把线段PC的长表示为![]() 的函数;
的函数;
(2)求四边形ACDP面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《高中数学课程标准》(2017版)规定了数学直观想象学科的六大核心素养,为了比较甲、乙两名高二学生的数学核心素养水平,现以六大素养为指标对二人进行了测验,根据测验结果绘制了雷达图(如图,每项指标值满分为5分,分值高者为优),则下面叙述正确的是(注:雷达图![]() ,又可称为戴布拉图、蜘蛛网图
,又可称为戴布拉图、蜘蛛网图![]() ,可用于对研究对象的多维分析)( )
,可用于对研究对象的多维分析)( )
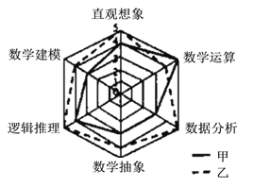
A.甲的直观想象素养高于乙
B.甲的数学建模素养优于数据分析素养
C.乙的数学建模素养与数学运算素养一样
D.乙的六大素养整体水平低于甲
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某单位的食堂中,食堂每天以10元/斤的价格购进米粉,然后以4.4元/碗的价格出售,每碗内含米粉0.2斤,如果当天卖不完,剩下的米粉以2元/斤的价格卖给养猪场.根据以往统计资料,得到食堂某天米粉需求量的频率分布直方图如图所示,若食堂购进了80斤米粉,以![]() (斤)(其中
(斤)(其中![]() )表示米粉的需求量,
)表示米粉的需求量, ![]() (元)表示利润.
(元)表示利润.
(1)估计该天食堂利润不少于760元的概率;
(2)在直方图的需求量分组中,以区间中间值作为该区间的需求量,以需求量落入该区间的频率作为需求量在该区间的概率,求![]() 的分布列和数学期望.
的分布列和数学期望.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com