
分析 (Ⅰ)由椭圆的方程及性质直接求解.
(Ⅱ)由椭圆的定义知$|P{F_1}|+|P{F_2}|=2a=2\sqrt{2}$①,勾股定理,得|PF1|2+|PF2|2=|F1F2|2=4c2②,①2-②,得|PF1|•|PF2|即可.
解答 解:(Ⅰ)由椭圆$C:\frac{x^2}{2}+{y^2}=1$知a2=2,b2=1,则$a=\sqrt{2},b=1$,故c=1---(2分)
所以椭圆C的长轴$2a=2\sqrt{2}$,短轴2b=2,离心率$e=\frac{c}{a}=\frac{1}{{\sqrt{2}}}=\frac{{\sqrt{2}}}{2}$,左焦点F1(-1,0).(6分)
(Ⅱ)解:由(Ⅰ)可得$a=\sqrt{2}$,b=1,c=1.
由椭圆的定义知$|P{F_1}|+|P{F_2}|=2a=2\sqrt{2}$①,-----------------------------(8分)
在Rt△PF1F2中,由勾股定理,得|PF1|2+|PF2|2=|F1F2|2=4c2②,①2-②,
得2|PF1|•|PF2|=8-4=4,--------------------------------------(10分)
∴|PF1|•|PF2|=2,∴S${\;}_{△{F}_{1}P{F}_{2}}$=$\frac{1}{2}$|PF1|•|PF2|=$\frac{1}{2}$×2=1.----------(12分)
点评 本题考查了椭圆的方程及焦点三角形的面积,属于基础题.


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案科目:高中数学 来源: 题型:选择题
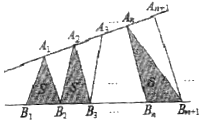 如图,点列{An},{Bn}分别在某个锐角的两边上,且|AnAn+1|=|An+1An+2|,An≠An+2,n∈N*,|BnBn+1|=|Bn+1Bn+2|,Bn≠Bn+2,n∈N*(P≠Q表示P与Q不重合).若dn=|AnBn|,Sn为△AnBnBn+1的面积,则( )
如图,点列{An},{Bn}分别在某个锐角的两边上,且|AnAn+1|=|An+1An+2|,An≠An+2,n∈N*,|BnBn+1|=|Bn+1Bn+2|,Bn≠Bn+2,n∈N*(P≠Q表示P与Q不重合).若dn=|AnBn|,Sn为△AnBnBn+1的面积,则( )| A. | {dn}是等差数列 | B. | {dn2}是等差数列 | C. | {Sn}是等差数列 | D. | {Sn2}是等差数列 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±$\frac{1}{2}$x | B. | y=±2x | C. | y=±$\frac{\sqrt{2}}{2}$x | D. | y=±$\sqrt{2}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
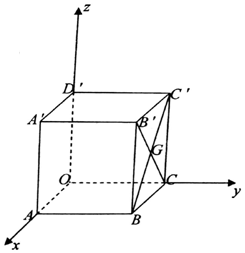 如图,棱长为1的正方体OABC-D′A′B′C′中,G为侧面正方形BCC′B′的中心,以顶点O为坐标原点建立如图所示的空间直角坐标系,则点G的坐标为($\frac{1}{2}$,1,$\frac{1}{2}$).
如图,棱长为1的正方体OABC-D′A′B′C′中,G为侧面正方形BCC′B′的中心,以顶点O为坐标原点建立如图所示的空间直角坐标系,则点G的坐标为($\frac{1}{2}$,1,$\frac{1}{2}$).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x}{2017x+1}$ | B. | $\frac{x}{x+2017}$ | C. | $\frac{2017x}{2017x+1}$ | D. | $\frac{2017x+1}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com