
【题目】设函数f(x)=ax+(k﹣1)a﹣x(a>且a≠1)是定义域为R的奇函数.
(1)求k值;
(2)若f(1)>0,试判断函数单调性,并求使不等式f(x2+x)+f(t﹣2x)>0恒成立的t的取值范围;
(3)若f(1)= ![]() ,设g(x)=a2x+a﹣2x﹣2mf(x),g(x)在[1,+∞)上的最小值为﹣1,求m的值.
,设g(x)=a2x+a﹣2x﹣2mf(x),g(x)在[1,+∞)上的最小值为﹣1,求m的值.
【答案】
(1)解:∵f(x)是定义域为R的奇函数;
∴f(0)=0;
∴k=0
(2)解:f(x)=ax﹣a﹣x(a>0,且a≠1);
由f(1)>0得 ![]() ;
;
∴a>1;
∴ax单调递增,a﹣x单调递减;
故f(x)在R上单调递增;
∵f(﹣x)=﹣f(x);
∴不等式化为f(x2+x)>f(2x﹣t);
∴x2+x>2x﹣t;
∴x2﹣x+t>0恒成立;
∴△=1﹣4t<0;
∴t的取值范围为 ![]()
(3)解:∵f(1)= ![]() ,∴
,∴ ![]() ;
;
即2a2﹣3a﹣2=0;
∴a=2,或a= ![]() (舍去);
(舍去);
∴g(x)=22x+2﹣2x﹣2m(2x﹣2﹣x)=(2x﹣2﹣x)2﹣2m(2x﹣2﹣x)+2;
令t=f(x)=2x﹣2﹣x,
由(2)可知f(x)=2x﹣2﹣x为增函数;
∵x≥1,∴t≥f(1)= ![]() ;
;
令h(t)=t2﹣2mt+2=(t﹣m)2+2﹣m2(t≥ ![]() )
)
①若m≥ ![]() ,当t=m时,h(t)min=2﹣m2=﹣1,∴m=
,当t=m时,h(t)min=2﹣m2=﹣1,∴m= ![]() ,∴m=
,∴m= ![]() ;
;
②若m< ![]() ,当t=
,当t= ![]() 时,h(t)min=
时,h(t)min= ![]() ﹣3m=﹣1,解得m=
﹣3m=﹣1,解得m= ![]() ,舍去;
,舍去;
综上可知m= ![]()
【解析】(1)根据f(x)为定义在R上的奇函数便有f(0)=0,从而可以求出k=0;(2)先得出f(x)=ax﹣a﹣x , 根据f(1)>0便可得出a>1,从而判断出f(x)为增函数,从而由原不等式可得x2﹣x+t>0恒成立,这便有△=1﹣4t<0,这样便可得出t的取值范围;(3)由f(1)= ![]() 便可求出a=2,从而可以得到g(x)=(2x﹣2﹣x)2﹣2m(2x﹣2﹣x)+2,可设t=f(x)=2x﹣2﹣x
便可求出a=2,从而可以得到g(x)=(2x﹣2﹣x)2﹣2m(2x﹣2﹣x)+2,可设t=f(x)=2x﹣2﹣x ![]() ,可令h(t)=(t﹣m)2+2﹣m2 , 该二次函数的对称轴为t=m,讨论m:
,可令h(t)=(t﹣m)2+2﹣m2 , 该二次函数的对称轴为t=m,讨论m: ![]() 时,t=m时,h(t)取到最小值2﹣m2=﹣1,这样便可求出m=
时,t=m时,h(t)取到最小值2﹣m2=﹣1,这样便可求出m= ![]() ;m
;m ![]() 时,t=
时,t= ![]() 时,h(t)取到最小值
时,h(t)取到最小值 ![]() ,得到m=
,得到m= ![]() ,不满足m
,不满足m ![]() ,从而便得到m的值只有一个为
,从而便得到m的值只有一个为 ![]() .
.


科目:高中数学 来源: 题型:
【题目】某品牌茶壶的原售价为80元/个,今有甲、乙两家茶具店销售这种茶壶,甲店用如下方法促销:如果只购买一个茶壶,其价格为78元/个;如果一次购买两个茶壶,其价格为76元/个;…,一次购买的茶壶数每增加一个,那么茶壶的价格减少2元/个,但茶壶的售价不得低于44元/个;乙店一律按原价的75%销售.现某茶社要购买这种茶壶x个,如果全部在甲店购买,则所需金额为y1元;如果全部在乙店购买,则所需金额为y2元.
(1)分别求出y1、y2与x之间的函数关系式;
(2)该茶社去哪家茶具店购买茶壶花费较少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.

(Ⅰ)求分数在[50,60)的频率及全班人数;
(Ⅱ)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间矩形的高;
(Ⅲ)若要从分数在[80,100)之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在[90,100)之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,x∈R,a∈R.
,x∈R,a∈R.
(1)a=1时,求证:f(x)在区间(﹣∞,0)上为单调增函数;
(2)当方程f(x)=3有解时,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三共有800名学生,为了解学生3月月考生物测试情况,根据男女学生人数差异较大,从中随机抽取了200名学生,记录他们的分数,并整理得如图频率分布直方图.
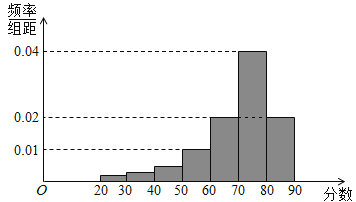
(1)若成绩不低于60分的为及格,成绩不低于80分的为优秀,试估计总体中合格的有多少人?优秀的有多少人?
(2)已知样本中有一半的女生分数不小于80,且样本中不低于80分的男女生人数之比2:3,试估计总体中男生和女生人数的比例.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x﹣ ![]() (x∈R).
(x∈R).
(1)讨论f(x)的奇偶性;
(2)若2xf(2x)+mf(x)≥0对任意的x∈[0,+∞)恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
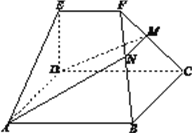
【题目】如图,在几何体![]() 中,底面
中,底面![]() 为矩形,
为矩形, ![]() ,
, ![]() .点
.点![]() 在棱
在棱![]() 上,平面
上,平面![]() 与棱
与棱![]() 交于点
交于点![]() .
.
(Ⅰ)求证: ![]() ;
;
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)若![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,求二面角
,求二面角![]() 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com