
����Ŀ����ƽ��ֱ������ϵxOy�ڣ�����P������F����1��0���ľ�����P����ֱ��x=��4�ľ���֮��Ϊ![]() .
.
��1����P�Ĺ켣C�ķ��̣�
��2�����켣C�ϵĶ���N������M��m��0����0��m��2���ľ������СֵΪ1����m��ֵ.
��3�����A��B�ǹ켣C���������㣬ֱ��OA��OB��켣C����һ����ֱ�ΪA1��B1����ֱ��OA��OB��б��֮������![]() �����ı���ABA1B1�����S�Ƿ�Ϊ��ֵ����˵������.
�����ı���ABA1B1�����S�Ƿ�Ϊ��ֵ����˵������.
���𰸡���1��![]() ����2��m=1����3���ǣ����ɼ�����.
����2��m=1����3���ǣ����ɼ�����.
��������
��1����P��x��y�������������빫ʽ�͵㵽ֱ�߾��빫ʽ���������P�Ĺ켣C�ķ��̣���2����N��x��y���������������빫ʽ�����m��
��3����һ����A��x1��y1����B��x2��y2������![]() ����
����![]() ���ɵ�A��B����ԲC�ϣ���
���ɵ�A��B����ԲC�ϣ���![]() ���ɴ����õ㵽ֱ�ߵľ��빫ʽ����Բ�ĶԳ��ԣ������֪����������ı���ABA1B1�����Ϊ��ֵ
���ɴ����õ㵽ֱ�ߵľ��빫ʽ����Բ�ĶԳ��ԣ������֪����������ı���ABA1B1�����Ϊ��ֵ![]() ��
��
��������A��x1��y1����B��x2��y2������A1����x1����y1����B1����x2����y2������![]() ����
����![]() ����A��B����ԲC�ϣ���
����A��B����ԲC�ϣ���![]() .�ɴ����õ㵽ֱ�ߵľ��빫ʽ����Բ�ĶԳ��ԣ������֪����������ı���ABA1B1�����Ϊ��ֵ
.�ɴ����õ㵽ֱ�ߵľ��빫ʽ����Բ�ĶԳ��ԣ������֪����������ı���ABA1B1�����Ϊ��ֵ![]() .
.
��1����P��x��y����
�߶���P������F����1��0���ľ�����P����ֱ��x=��4�ľ���֮��Ϊ![]() ��
��
�������⣬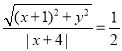 �������3x2+4y2=12��
�������3x2+4y2=12��
�ද��P�Ĺ켣C�ķ���Ϊ![]() ��
��
��2����N��x��y������![]()
![]() ����2��x��2.
����2��x��2.
�ٵ�0��4m��2����![]() ʱ����x=4mʱ��|MN|2ȡ��Сֵ3��1��m2��=1��
ʱ����x=4mʱ��|MN|2ȡ��Сֵ3��1��m2��=1��
���![]() ��
��![]() ����ʱ
����ʱ![]() ������ȥ.
������ȥ.
�ڵ�4m��2����![]() ʱ����x=2ʱ��|MN|2ȡ��Сֵm2��4m+4=1��
ʱ����x=2ʱ��|MN|2ȡ��Сֵm2��4m+4=1��
���m=1����m=3���ᣩ.
���ϣ�m=1.
��3���ⷨһ����A��x1��y1����B��x2��y2����
����![]() ����
����![]() ��
��![]() ��
��
�ߵ�A��B����ԲC�ϣ���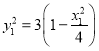 ��
��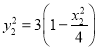 ��
��
��![]() �������
�������![]() .
.
�ٵ�x1=x2ʱ�����ı���ABA1B1Ϊ���Σ�y2=��y1����![]() ��
��
��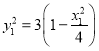 ����
����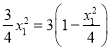 �����
�����![]() ��
��![]() ��
��
![]()
![]() .
.
�ڵ�x1��x2ʱ��ֱ��AB�ķ�������Ϊ![]() ��
��
ֱ��AB�ķ���Ϊ![]() ��
��
ԭ��O��ֱ��AB�ľ���Ϊ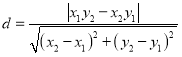
���AOB�����![]() ��
��
������Բ�ĶԳ��ԣ��ı���ABA1B1�����S=4S��AOB=2|x1y2��x2y1|��
��![]()
=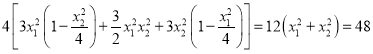 ����
����![]() .
.
���ı���ABA1B1�����Ϊ��ֵ![]() .
.
�ⷨ������A��x1��y1����B��x2��y2������A1����x1����y1����B1����x2����y2����
��![]() ����
����![]() ��
��
�ߵ�A��B����ԲC�ϣ�����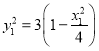 ��
��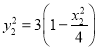 ��
��
��![]() �������
�������![]() .
.
ֱ��OA�ķ���Ϊy1x��x1y=0����B��ֱ��OA�ľ���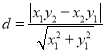 ��
��
��ABA1�����![]() ��
��
������Բ�ĶԳ��ԣ��ı���ABA1B1�����![]() =2|x1y2��x2y1|��
=2|x1y2��x2y1|��
��![]()
=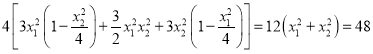 ����
����![]() .
.
���ı���ABA1B1�����Ϊ��ֵ![]() .
.


 һ��һ��һ��ͨϵ�д�
һ��һ��һ��ͨϵ�д� �㽭֮��ѧҵˮƽ����ϵ�д�
�㽭֮��ѧҵˮƽ����ϵ�д� ��Ч���ܿ�ʱ��ҵϵ�д�
��Ч���ܿ�ʱ��ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ![]() ��Բ
��Բ![]() ����ԲP��ԲM���в�����ԲN���У�Բ��P�Ĺ켣Ϊ����C.
����ԲP��ԲM���в�����ԲN���У�Բ��P�Ĺ켣Ϊ����C.
��1��������C�ķ��̣�
��2���費������![]() ��ֱ��l������C�ཻ��A��B���㣬ֱ��QA��ֱ��QB��б�ʾ�������б��֮��Ϊ-2��֤����ֱ��l������.
��ֱ��l������C�ཻ��A��B���㣬ֱ��QA��ֱ��QB��б�ʾ�������б��֮��Ϊ-2��֤����ֱ��l������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���ԲC������������ԭ��O�����ҽ���Ϊ![]() ���ҵ�
���ҵ�![]() ����ԲC�ϣ�
����ԲC�ϣ�

![]() ����ԲC�ķ��̣�
����ԲC�ķ��̣�
![]() ����Բ�����Ҷ���ֱ�ΪA��B��M����Բ������A��B������һ�㣬ֱ��MF����ԲC����һ��N��ֱ��MB��ֱ��
����Բ�����Ҷ���ֱ�ΪA��B��M����Բ������A��B������һ�㣬ֱ��MF����ԲC����һ��N��ֱ��MB��ֱ��![]() ��Q�㣬��֤��A��N��Q������ͬһ��ֱ���ϣ�
��Q�㣬��֤��A��N��Q������ͬһ��ֱ���ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ѧ��Ϊ��ӭ�Ӹ߿���Ҫ��������ģ�⿼�ԣ�����Ӧ��������ijѧ��������������߿�Ҫ�μ�![]() ��ģ�⿼�ԣ������Ǹ�����һѧ��ijѧ���μ�
��ģ�⿼�ԣ������Ǹ�����һѧ��ijѧ���μ�![]() ��ģ�⿼�Ե���ѧ�ɼ�����
��ģ�⿼�Ե���ѧ�ɼ�����
ģ�⿼�Ե� |
|
|
|
|
|
���Գɼ� |
|
|
|
|
|
��1����֪�ÿ�����ģ�⿼�Գɼ�![]() ��ģ�⿼�ԵĴ���
��ģ�⿼�ԵĴ���![]() ����ع�ֱ�߷���
����ع�ֱ�߷���![]() �����߿�������
�����߿�������![]() ��ģ�⿼�ԣ��Թ��Ƹÿ����ĸ߿���ѧ�ɼ���
��ģ�⿼�ԣ��Թ��Ƹÿ����ĸ߿���ѧ�ɼ���
��2����![]() ��ģ�⿼�Եijɼ������������ͬ���ŷ��У����������ȡ
��ģ�⿼�Եijɼ������������ͬ���ŷ��У����������ȡ![]() ���ŷ��о��ɼ������ȡ��
���ŷ��о��ɼ������ȡ��![]() ���ŷ���ǡ��
���ŷ���ǡ��![]() ���ɼ�������ƽ��ֵ
���ɼ�������ƽ��ֵ![]() �ĸ���.
�ĸ���.
�ο���ʽ�� ��
��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���ij������������8��̨����ȵ����������������20̨����������ʹ��ʱ�ޣ���λ��Сʱ�� ���£�
248 256 232 243 188 268 278 266 289 312
274 296 288 302 295 228 287 217 329 283
���� | Ƶ�� | Ƶ�� | Ƶ��/��� |
| |||
| |||
| |||
| |||
| |||
| |||
| |||
| |||
�ܼ� | 0.05 |
��1�����Ƶ�ʷֲ�����������Ƶ�ʷֲ�ֱ��ͼ��
��2������8��̨��������ж���̨��������ʹ��ʱ������280Сʱ��
��3��������ֵ��ͬһ���е������ڸ���������е�ֵ������������ƽ����������ʹ��ʱ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ĸ����⣺����������ֱ�߶�����ȷ��һ��ƽ�棻��������ƽ����3����ͬ�Ĺ����㣬��������ƽ���غϣ���ֱ��a��b��c����a��b���棬b��c���棬��a��c���棻����ֱ��l����һ����ƽ�����⣬��l��ƽ������.���д�������ĸ����ǣ�������
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() ���߷���Ϊ
���߷���Ϊ![]() ��ֱ��
��ֱ��![]() ������
������![]() ��
��![]() �����������߽���
�����������߽���![]() ��
��![]() ���㣬
���㣬![]() Ϊ����ԭ��.
Ϊ����ԭ��.
��1���������ߵķ��̣�
��2��![]() �Ƿ�Ϊ��ֵ�����ǣ���������ֵ�������ǣ���˵�����ɣ�
�Ƿ�Ϊ��ֵ�����ǣ���������ֵ�������ǣ���˵�����ɣ�
��3����![]() ʱ����
ʱ����![]() ����
����![]() ����
����![]() �Ľ���ʽ.
�Ľ���ʽ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����������ָ��ֵΪ������ָ��ֵΪ8ʱ��Ϊ�ϸ�Ʒ��ָ��ֵΪ7����9ʱ��Ϊ�ϸ�Ʒ��ָ��ֵΪ6��10ʱ��Ϊ��Ʒ��ij��λӵ��һ̨���������Ļ�����Ϊ���˽�������ܣ������ȡ�˸û��������100���������ͬ������ָ��ֵ��Ӧ������������±���ʾ��
����ָ��ֵ | 6 | 7 | 8 | 9 | 10 |
������� | 6 | 18 | 60 | 12 | 4 |
ʹ�øû��������һ������ɱ�Ϊ5Ԫ���ϸ�Ʒ������ÿ��![]() Ԫ�ļ۸���۸������̣��ϸ�Ʒ���Ʒ������.
Ԫ�ļ۸���۸������̣��ϸ�Ʒ���Ʒ������.
��1�����Ƹû����������������ָ��ֵ��ƽ������
��2�����õ�λ�ӵ�һ�Ŷ�������Ҫ�����2100����Ϊʹ�˴ν������ﵽ1400Ԫ������![]() ����Сֵ��
����Сֵ��
��3���õ�λ������һ̨�ӹ��豸��ÿ���������2Ԫ���Ա��ӹ�һ�Σ��ӹ������ȿ��ܳ����������������������ָ��ֵ����1��������ָ��ֵ���䣬������ָ��ֵ����1.��֪ÿ��������ɱ��ӹ�һ�Σ��Ҹõ�λ�ƻ��������ϸ�Ʒ��һ�ӹ����ڣ�2���������£�����![]() ����Сֵ����ȷ��0.01�� .
����Сֵ����ȷ��0.01�� .
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com