
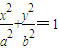 与双曲线
与双曲线 具有相同的焦点F1,F2,且顶点P(0,b)满足
具有相同的焦点F1,F2,且顶点P(0,b)满足 .
.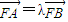 ,求实数λ的范围.
,求实数λ的范围.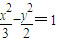 的焦点F1(-
的焦点F1(-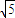 ,0),F2(
,0),F2(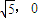 ),知椭圆
),知椭圆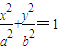 的焦点F1(-
的焦点F1(-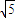 ,0),F2(
,0),F2(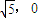 ),由此能求出椭圆的方程.
),由此能求出椭圆的方程.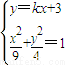 ,得(4+9k2)x2+54kx+45=0,设A(x1,y1),B(x2,y2),由
,得(4+9k2)x2+54kx+45=0,设A(x1,y1),B(x2,y2),由 ,知
,知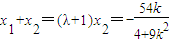 ,
,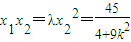 ,由此能求出实数λ的范围.
,由此能求出实数λ的范围.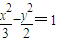 的焦点F1(-
的焦点F1(-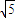 ,0),F2(
,0),F2(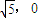 ),
),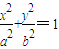 的焦点F1(-
的焦点F1(-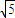 ,0),F2(
,0),F2(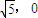 ),
),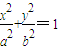 的顶点P(0,b)满足
的顶点P(0,b)满足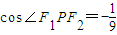 ,
,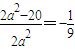 ,
,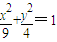 .
.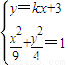 ,
,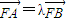 ,
,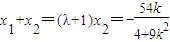 ,①
,①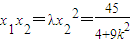 ,②
,②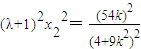 ,③
,③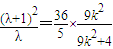 ,
, ,
,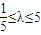 .
.

科目:高中数学 来源:2005-2006学年江苏省南通市高二(上)期末数学试卷(解析版) 题型:填空题
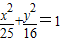 与双曲线
与双曲线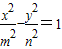 (m>0,n>0)具有相同的焦点F1,F2,设两曲线的一个交点为Q,∠QF1F2=90°,则双曲线的离心率为 .
(m>0,n>0)具有相同的焦点F1,F2,设两曲线的一个交点为Q,∠QF1F2=90°,则双曲线的离心率为 .查看答案和解析>>
科目:高中数学 来源:2006-2007学年江苏省南通市如东县高二(上)期末数学试卷(解析版) 题型:填空题
 与双曲线
与双曲线 (m>0,n>0)具有相同的焦点F1,F2,设两曲线的一个交点为Q,∠QF1F2=90°,则双曲线的离心率为 .
(m>0,n>0)具有相同的焦点F1,F2,设两曲线的一个交点为Q,∠QF1F2=90°,则双曲线的离心率为 .查看答案和解析>>
科目:高中数学 来源:2005-2006学年江苏省常州市武进区前黄高中高二(上)期末数学试卷(解析版) 题型:填空题
 与双曲线
与双曲线 (m>0,n>0)具有相同的焦点F1,F2,设两曲线的一个交点为Q,∠QF1F2=90°,则双曲线的离心率为 .
(m>0,n>0)具有相同的焦点F1,F2,设两曲线的一个交点为Q,∠QF1F2=90°,则双曲线的离心率为 .查看答案和解析>>
科目:高中数学 来源:2011年高三数学精品复习16:双曲线及其性质(解析版) 题型:解答题
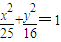 与双曲线
与双曲线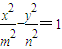 (m>0,n>0)具有相同的焦点F1,F2,设两曲线的一个交点为Q,∠QF1F2=90°,则双曲线的离心率为 .
(m>0,n>0)具有相同的焦点F1,F2,设两曲线的一个交点为Q,∠QF1F2=90°,则双曲线的离心率为 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com