
| 天数x(天) | 3 | 5 | 7 | 9 | 11 | 13 | 15 |
| 日经济收入Q(万元) | 154 | 180 | 198 | 208 | 210 | 204 | 190 |
分析 (1)由提供的数据知道,描述宾馆日经济收入Q与天数的变化关系的函数不可能为常数函数,也不可能是单调函数,故选取二次函数Q=-x2+ax+b进行描述,将(3,154)、(5,180)代入Q=-x2+ax+b,代入Q,即得函数解析式;
(2)由二次函数的图象与性质,利用配方法可求取最值.
解答 解:(1)由提供的数据知道,描述宾馆日经济收入Q与天数的变化关系的函数不可能为常数函数,从而用四个中的任意一个进行描述时都应有,
而Q=at+b,Q=ax+b,Q=b+logax三个函数均为单调函数,这与表格所提供的数据不符合,
∴选取二次函数进行描述最恰当;
将(3,154)、(5,180)代入Q=-x2+ax+b,
可得$\left\{\begin{array}{l}{154=-9+3a+b}\\{180=-25+5a+b}\end{array}\right.$,解得a=21,b=100.
∴Q=-x2+21x+100,(1≤x≤20,x∈N*);
(2)Q=-x2+21x+100=-(t-$\frac{21}{2}$)2+$\frac{841}{4}$,
∵1≤x≤20,x∈N*,
∴t=10或11时,Q取得最大值210万元.
点评 本题考查了二次函数模型的应用,考查利用二次函数的图象与性质求函数的最值问题,确定函数模型是关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题

| A. | 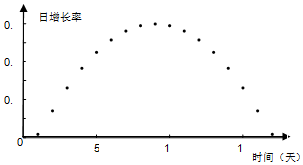 | |
| B. | 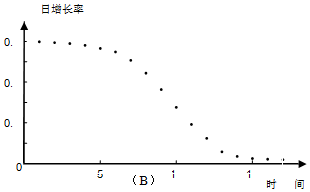 | |
| C. | 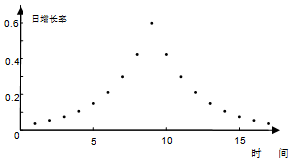 | |
| D. | 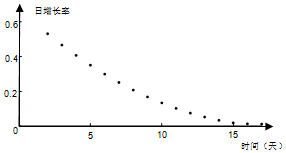 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 即不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
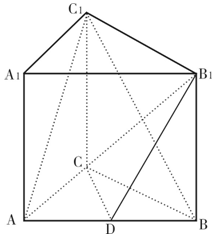 如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=3,BC=4,AB=5,点D是AB的中点.
如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=3,BC=4,AB=5,点D是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
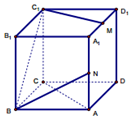 如图,已知正方体ABCD-A1B1C1D1,M,N分别为A1D1和AA1的中点,则下列四种说法中正确的个数为( )
如图,已知正方体ABCD-A1B1C1D1,M,N分别为A1D1和AA1的中点,则下列四种说法中正确的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
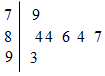 如图是2013年中央电视台举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
如图是2013年中央电视台举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )| A. | 85,1.6 | B. | 84,4 | C. | 84,1.6 | D. | 85,4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
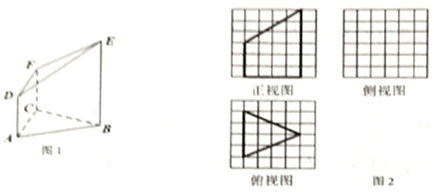
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,使得x2-2x-3>0成立 | B. | ?x0∈R,使得x2-2x-3≥0成立 | ||
| C. | ?x∈R,x2-2x-3<0恒成立 | D. | ?x∈R,x2-2x-3≥0恒成立 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com