
分析 若方程-x2+5x+m=5-x,在x∈(0,5)内有唯一解,即方程x2+6x+m-5=0在x∈(0,5)内有唯一解,分别讨论△=0和△>0时,满足条件的实数m的值,最后综合讨论结果可得答案.
解答 解:若方程-x2+5x+m=5-x,在x∈(0,5)内有唯一解,
即方程-x2+6x+m-5=0在x∈(0,5)内有唯一解,
若△=36+4(m-5)=0,即m=-4,
此时方程有唯一解3∈(0,5)满足要求,
若△=36+4(m-5)>0,即m>-4,
此时方程有唯一解,即函数f(x)=-x2+6x+m-5,在x∈(0,5)内有唯一的零点,
即f(0)f(5)=(m-5)•m<0,满足条件的m值为:(0,5),
综上所述实数m的取值范围是:{-4}∪(0,5).
故答案为:{-4}∪(0,5).
点评 本题考查的知识点:二次函数的性质,方程的根与函数的零点,其中熟练掌握函数的零点与对应方程根之间的关系是解答的关键.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年云南大理州南涧县民族中学高二文9月月考数学试卷(解析版) 题型:选择题
设f(x)是周期为2的奇函数,当0≤x≤1时,f(x)=2x(1-x),则f(- )等于( )
)等于( )
A.-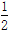 B.-
B.- C.
C.  D.
D. 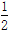
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com