
2013年9月20日是第25个全国爱牙日。某区卫生部门成立了调查小组,调查 “常吃零食与患龋齿的关系”,对该区六年级800名学生进行检查,按患龋齿和不患龋齿分类,得汇总数据:不常吃零食且不患龋齿的学生有60名,常吃零食但不患龋齿的学生有100名,不常吃零食但患龋齿的学生有140名.
(1)能否在犯错概率不超过0.001的前提下,认为该区学生的常吃零食与患龋齿有关系?
(2)4名区卫生部门的工作人员随机分成两组,每组2人,一组负责数据收集,另一组负责数据处理.求工作人员甲分到负责收集数据组,工作人员乙分到负责数据处理组的概率.
 | 0.010 | 0.005 | 0.001 |
 | 6.635 | 7.879 | 10.828 |

(1)学生常吃零食与患龋齿有关系(2)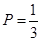
解析试题分析:(1)根据题意建立相应的列联表,根据公式
科目:高中数学
来源:
题型:解答题
设袋子中装有a个红球,b个黄球,c个蓝球,且规定:取出一个红球得1分,取出一个黄球得2分,取出一个蓝球得3分.
科目:高中数学
来源:
题型:解答题
某商店试销某种商品20天,获得如下数据:
科目:高中数学
来源:
题型:解答题
一个口袋中有
科目:高中数学
来源:
题型:解答题
2014年2月21日,《中共中央关于全面深化改革若干重大问题的决定》明确:坚持计划生育的基本国策,启动实施一方是独生子女的夫妇可生育两个孩子的政策.为了解某地区城镇居民和农村居民对“单独两孩”的看法,某媒体在该地区选择了3600人调查,就是否赞成“单独两孩”的问题,调查统计的结果如下表:
科目:高中数学
来源:
题型:解答题
在高中“自选模块”考试中,某考场的每位同学都选了一道数学题,第一小组选《数学史与不等式选讲》的有1人,选《矩阵变换和坐标系与参数方程》的有5人,第二小组选《数学史与不等式选讲》的有2人,选《矩阵变换和坐标系与参数方程》的有4人,现从第一、第二两小组各任选2人分析得分情况.
科目:高中数学
来源:
题型:解答题
生产A,B两种元件,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品,现随机抽取这两种元件各100件进行检测,检测结果统计如下:
科目:高中数学
来源:
题型:解答题
1号箱中有2个白球和4个红球,2号箱中有5个白球和3个红球,现随机地从1号箱中取出一球放入2号箱,然后从2号箱随机取出一球,问从2号箱取出红球的概率是多少?
科目:高中数学
来源:
题型:解答题
第17届亚运会将于2014年9月18日至10月4日在韩国仁川进行,为了搞好接待工作,组委会招募了16名男志愿者和14名女志愿者,调查发现,男、女志愿者中分别有10人和6人喜爱运动,其余不喜爱.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区 计算
计算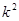 ,查表比较大小即可判断是否有关
,查表比较大小即可判断是否有关
(2)古典概型,对四名工作人员编号,利用树状图或者表格的方式列出四选两个的所有基本事件,求出符合“工作人员甲分到负责收集数据组,工作人员乙分到负责数据处理组”的基本事件数,根据古典概型概率的计算公式即可得到相应的概率.
试题解析:(1)由题意可得列联表:
因为 不常吃零食 常吃零食 总计 不患龋齿 60 100 160 患龋齿 140 500 640 总计 200 600 800  。
。
所以能在犯错率不超过0.001的前提下,为该区学生常吃零食与患龋齿有关系。
(2)设其他工作人员为丙和丁,4人分组的所有情况如下表小组 1 2 3 4 5 6 收集数据 甲乙 甲丙 甲丁 乙丙 乙丁 丙丁 处理数据 丙丁 

小学生家庭作业系列答案
考易通课时全优练系列答案
与名师对话同步单元测试卷系列答案
黄冈状元笔记系列答案
练习册吉林教育出版集团有限责任公司系列答案
练习册湖北教育出版社系列答案
新课标同步练习系列答案
实验作业系列答案
组合训练湖北教育出版社系列答案
伴你快乐成长开心作业系列答案
(1)当a=3,b=2,c=1时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量ξ为取出此两球所得分数之和,求ξ分布列;
(2)从该袋子中任取(且每球取到的机会均等)1个球,记随机变量η为取出此球所得分数.若E(η)= ,V(η)=
,V(η)= ,求a∶b∶c.
,求a∶b∶c.
试销结束后(假设该商品的日销售量的分布规律不变).设某天开始营业时由该商品3件,当天营业结束后检查存货,若发现存量少于2件,则当天进货补充至3件,否则不进货,将频率视为概率.日销售量(件) 0 1 2 3 频数 1 5 9 5
(1)求当天商店不进货的概率;
(2)记X为第二天开始营业时该商品视为件数,求X的分布列和数学期望. 个白球和
个白球和 个红球(
个红球( ,且
,且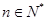 ),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
(1)试用含 的代数式表示一次摸球中奖的概率
的代数式表示一次摸球中奖的概率 ;
;
(2)若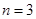 ,求三次摸球恰有一次中奖的概率;
,求三次摸球恰有一次中奖的概率;
(3)记三次摸球恰有一次中奖的概率为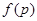 ,当
,当 为何值时,
为何值时,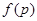 取最大值.
取最大值.
已知在全体样本中随机抽取1人,抽到持“反对”态度的人的概率为0.05.
赞成
反对
无所谓
农村居民
2100人
120人
y人
城镇居民
600人
x人
z人
(1)现在分层抽样的方法在所有参与调查的人中抽取360人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(2)在持“反对”态度的人中,用分层抽样的方法抽取6人,按每组3人分成两组进行深入交流,求第一组中农村居民人数 的分布列和数学期望.
的分布列和数学期望.
(1)求选出的4人均为选《矩阵变换和坐标系与参数方程》的概率;
(2)设X为选出的4个人中选《数学史与不等式选讲》的人数,求X的分布列和数学期望.
(1)试分别估计元件A、元件B为正品的概率;测试指标 [70,76) [76,82) [82,88) [88,94) [94,100] 元件A 8 12 40 32 8 元件B 7 18 40 29 6
(2)生产一件元件A,若是正品可盈利50元,若是次品则亏损10元;生产一件元件B,若是正品可盈利100元,若是次品则亏损20元,在(1)的前提下:
(i)求生产5件元件B所获得的利润不少于300元的概率;
(ii)记X为生产1件元件A和1件元件B所得的总利润,求随机变量X的分布列和数学期望.
(1)根据调查数据制作2×2列联表;
(2)根据列联表的独立性检验,能否认为性别与喜爱运动有关?
(参考公式:参考数据 当 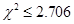 时,无充分证据判定变量
时,无充分证据判定变量 有关联,可以认为两变量无关联;
有关联,可以认为两变量无关联;当  时,有
时,有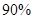 把握判定变量
把握判定变量 有关联;
有关联;当 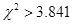 时,有
时,有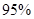 把握判定变量
把握判定变量 有关联;
有关联;当 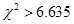 时,有
时,有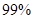 把握判定变量
把握判定变量 有关联.
有关联. ,其中
,其中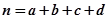 .)
.)
版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。
ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号