
 ,点B是
,点B是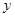 轴上的动点,过B作AB的垂线
轴上的动点,过B作AB的垂线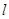 交
交 轴于点Q,若
轴于点Q,若 ,
, .
.
 ,以PM为直径的圆与直线
,以PM为直径的圆与直线 的相交弦长为定值,若存在,求出定直线方程;若不存在,请说明理由。
的相交弦长为定值,若存在,求出定直线方程;若不存在,请说明理由。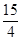 ,以PM为直径的圆与直线x=
,以PM为直径的圆与直线x=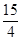 的相交弦长为定值
的相交弦长为定值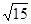 。
。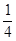 |m|,
|m|,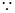 m
m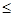 0,m=-4t2,
0,m=-4t2, Q(-4t2,0),设P(x,y),则
Q(-4t2,0),设P(x,y),则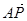 =(x-
=(x-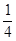 ,y),
,y),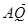 =(-4t2-
=(-4t2-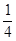 ,0),2
,0),2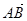 =(-
=(-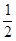 ,2 t),
,2 t), 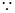
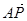 +
+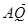 =2
=2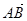 。
。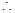 (x-
(x-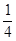 ,y)+ (-4t2-
,y)+ (-4t2-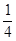 ,0)= (-
,0)= (-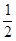 ,2 t),
,2 t),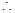 x=4t2,y="2" t,
x=4t2,y="2" t,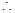 y2=x,此即点P的轨迹方程; 6分。
y2=x,此即点P的轨迹方程; 6分。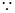 M (4,0) ,则以PM为直径的圆的圆心即PM的中点T(
M (4,0) ,则以PM为直径的圆的圆心即PM的中点T(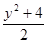 ,
,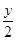 ), 以PM为直径的圆与直线x=a的相交弦长:
), 以PM为直径的圆与直线x=a的相交弦长: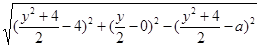
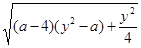 =2
=2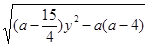 10分
10分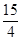 ="0," 即a=
="0," 即a=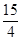 时,L=
时,L=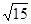
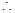 存在定直线x=
存在定直线x=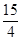 ,以PM为直径的圆与直线x=
,以PM为直径的圆与直线x=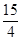 的相交弦长为定值
的相交弦长为定值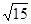 。13分
。13分

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com