练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．命题“若实数a满足a≤3，则a2＜9”的否命题是真命题（填“真”、“假”之一）．

    分析 写出该命题的否命题并判断真假．

    解答 解：命题“若实数a满足a≤3，则a2＜9”的否命题是
    “若实数a满足a＞3，则a2≥9”，
    它是真命题，因为a＞3时，a2＞9，
    ∴a2≥9成立．
    故答案为：真．

    点评 本题考查了四种命题之间的应用问题，也考查了命题真假的判断问题，是基础题目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    3．下列说法正确的是（　　）
    A．某人打靶，射击10次，击中7次，那么此人中靶的概率为0.7
    B．一位同学做掷硬币试验，掷6次，一定有3次“正面朝上”
    C．某地发行福利彩票，回报率为47%，有人花了100元钱买彩票，一定会有47元的回报
    D．概率等于1的事件不一定为必然事件

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．已知数列{an}的前n项和${S_n}={n^2}-4n+1$，则a1+a2+a3+…+a10=61．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．函数$y=\frac{ln（2x-1）}{{\sqrt{2-x}}}$的定义域为（　　）
    A．（$\frac{1}{2}$，+∞）B．（$\frac{1}{2}$，2）C．（$\frac{1}{2}$，1）D．（-∞，2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

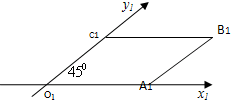    8．如图，一个正方形OABC在斜二测画法下的直观图是个一条边长为1的平行四边形，则正方形OABC的面积为（　　）
    A．1B．4C．1或4D．不能确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知方程lnx-ax+1=0（a为实常数）有两个不等实根，则实数a的取值范围是（　　）
    A．（0，e）B．[1，e]C．（0，1）D．[0，1]

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．若函数f（x）唯一的一个零点同时在区间（0，8）、（0，6）、（0，4）、（0，2）内，那么下列命题中正确的是（　　）
    A．函数f（x）在区间（0，1）内有零点B．函数f（x）在区间（0，1）或（1，2）内有零点
    C．函数f（x）在区间[2，8）内无零点D．函数f（x）在区间（1，8）内无零点

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知函数$f（x）=-\frac{3}{2}{x^2}+ax-1$；
    （1）若函数f（x）在（-∞，+∞）上至少有一个零点，求a的取值范围；
    （2）求函数f（x）在[1，2]上的最大值；
    （3）若函数g（x）=f（x）+1在R上的最大值不大于$\frac{1}{6}$，又当$x∈[\frac{1}{4}，\frac{1}{2}]$时，$f（x）≥\frac{1}{8}$，求a得值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知函数f（x）=$\frac{1-x}{ax}$+lnx
    （1）若函数f（x）在[1，+∞）上为增函数，求正实数a的取值范围；
    （2）当a=1时，求函数f（x）在[$\frac{1}{2}$，2]上的最值；
    当a=1时，对大于1的任意正整数n，试比较ln$\frac{n}{n-1}$与$\frac{1}{n}$的大小关系．

    查看答案和解析>>

    同步练习册答案