
【题目】已知函数![]() .
.
(Ⅰ)讨论函数![]() 的单调性;
的单调性;
(Ⅱ)记函数![]() 的两个零点分别为
的两个零点分别为![]() ,且
,且![]() .已知
.已知![]() ,若不等式
,若不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)函数![]() 在
在![]() 上单调递增;在
上单调递增;在![]() 上单调递减; (Ⅱ)
上单调递减; (Ⅱ)![]() .
.
【解析】试题分析:(Ⅰ)求出函数的导数,通过讨论![]() 的范围,求出函数 的单调区间即可; (Ⅱ)分离参数得:
的范围,求出函数 的单调区间即可; (Ⅱ)分离参数得: ![]() ,从而可得
,从而可得![]() 恒成立;再令
恒成立;再令![]() ,从而可得不等式
,从而可得不等式![]() 在
在![]() 上恒成立,再令
上恒成立,再令![]() ,从而利用导数化恒成立问题为最值问题即可.
,从而利用导数化恒成立问题为最值问题即可.
试题解析:(Ⅰ)依题意,函数![]() 的定义域为
的定义域为![]() ,
,
![]() ,
,
当![]() 时,
时, ![]() 恒成立,故函数
恒成立,故函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,令
时,令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]() ;
;
故函数![]() 在
在![]() 上单调递增;在
上单调递增;在![]() 上单调递减,
上单调递减,
(Ⅱ)由(I)可知![]() 分别为方程
分别为方程![]() 的两个根,即
的两个根,即![]() ,
, ![]() ,
,
所以原式等价于![]() .
.
因为![]() ,
, ![]() ,所以原式等价于
,所以原式等价于![]() ,
,
又由![]() ,
, ![]() 作差得,
作差得, ![]() ,即
,即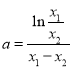 .
.
所以原式等价于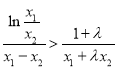 .
.
因为![]() ,原式恒成立,即
,原式恒成立,即![]() 恒成立.
恒成立.
令![]() ,则不等式
,则不等式![]() 在
在![]() 上恒成立.
上恒成立.
令![]() ,则
,则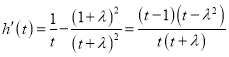 ,
,
当![]() 时,可见
时,可见![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上单调递增,又
上单调递增,又![]() 在
在![]() 恒成立,符合题意;
恒成立,符合题意;
当![]() 时,可见当
时,可见当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,
,
所以![]() 在
在![]() 时单调递增,在
时单调递增,在![]() 时单调递减.
时单调递减.
又![]() ,所以
,所以![]() 在
在![]() 上不能恒小于0,不符合题意,舍去.
上不能恒小于0,不符合题意,舍去.
综上所述,若不等式![]() 恒成立,只须
恒成立,只须![]() ,又
,又![]() ,所以
,所以![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,x∈R.
,x∈R.
(1)分别求出f(2)+f( ![]() ),f(3)+f(
),f(3)+f( ![]() ),f(4)+f(
),f(4)+f( ![]() )的值;
)的值;
(2)根据(1)归纳猜想出f(x)+f( ![]() )的值,并证明.
)的值,并证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=3|x+2|﹣|x﹣4|.
(1)求不等式f(x)>2的解集;
(2)设m,n,k为正实数,且m+n+k=f(0),求证:mn+mk+nk≤ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)是定义在R上的奇函数,且在(﹣∞,0]上满足 ![]() <0,且f(1)=0,则使得
<0,且f(1)=0,则使得 ![]() <0的x的取值范围是( )
<0的x的取值范围是( )
A.(﹣∞,1)
B.(﹣∞,﹣1)∪(1,+∞)
C.(﹣1,0)∪(1,+∞)
D.(﹣1,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.
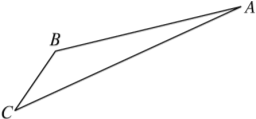
现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50 m/min,在甲出发2 min后,乙从A乘缆车到B,在B处停留1 min后,再从B匀速步行到C.假设缆车匀速直线运行的速度为130 m/min,山路AC长为1 260 m,经测量,cos A=![]() ,cos C=
,cos C=![]() .
.
(1)求索道AB的长;
(2)问乙出发多少分钟后,乙在缆车上与甲的距离最短?
(3)为使两位游客在C处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=x2﹣bx+3.
(1)若函数f(x)为R上的偶函数,求b的值.
(2)若函数f(x)在(﹣∞,2]上单调递减,求b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com