
 有两个极值点
有两个极值点 ,且
,且 ,则 ( )
,则 ( )A. | B.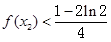 |
C.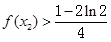 | D. |
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 其中2<x<6,m为常数,已知销售价格为4元/件时,每月可售出21千件。(1)求m的值; (2)假设该淘宝店员工工资、办公等每月所有开销折合为每件2元(只考虑销售出的件数),试确定销售价格x的值,使该店每月销售饰品所获得的利润最大.(结果保留一位小数)
其中2<x<6,m为常数,已知销售价格为4元/件时,每月可售出21千件。(1)求m的值; (2)假设该淘宝店员工工资、办公等每月所有开销折合为每件2元(只考虑销售出的件数),试确定销售价格x的值,使该店每月销售饰品所获得的利润最大.(结果保留一位小数)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 名工人,现接受了生产
名工人,现接受了生产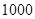 台
台 型高科技产品的总任务.已知每台
型高科技产品的总任务.已知每台 型产品由
型产品由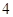 个
个 型装置和
型装置和 个
个 型装置配套组成,每个工人每小时能加工
型装置配套组成,每个工人每小时能加工 个
个 型装置或
型装置或 个
个 型装置.现将工人分成两组同时开始加工,每组分别加工一种装置(完成自己的任务后不再支援另一组).设加工
型装置.现将工人分成两组同时开始加工,每组分别加工一种装置(完成自己的任务后不再支援另一组).设加工 型装置的工人有
型装置的工人有 人,他们加工完
人,他们加工完 型装置所需时间为
型装置所需时间为 ,其余工人加工完
,其余工人加工完 型装置所需时间为
型装置所需时间为 (单位:小时,可不为整数).
(单位:小时,可不为整数). 、
、 的解析式;
的解析式; 名工人完成总任务的时间
名工人完成总任务的时间 的解析式;
的解析式;查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 ,
, )的切线的斜率为
)的切线的斜率为
 的最小值为
的最小值为
 轴有4个交点
轴有4个交点 在
在 上为减函数,在
上为减函数,在 上也为减函数
上也为减函数查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
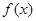 的定义域为
的定义域为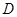 ,若满足:①
,若满足:①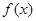 在
在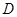 内是单调函数; ②存在
内是单调函数; ②存在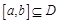
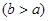 ,使得
,使得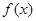 在
在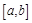 上的值域为
上的值域为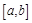 ,那么就称
,那么就称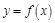 是定义域为
是定义域为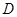 的“成功函数”.若函数
的“成功函数”.若函数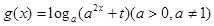 是定义域为
是定义域为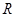 的“成功函数”,则
的“成功函数”,则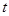 的取值范围为 ( )
的取值范围为 ( )A. | B. | C. | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
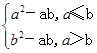 ,设f(x)=(2x-1)﹡x,且关于x 的方程f(x)=m(m∈R)恰有三个互不相等的实数根
,设f(x)=(2x-1)﹡x,且关于x 的方程f(x)=m(m∈R)恰有三个互不相等的实数根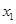 ,
,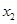 ,
,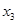 ,则
,则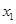 +
+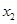 +
+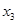 的取值范围是___________.
的取值范围是___________.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
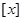 表示不超过
表示不超过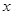 的最大整数,例如
的最大整数,例如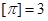 ,
,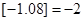 ,定义函数
,定义函数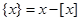 ,给出下列四个命题:(1)函数
,给出下列四个命题:(1)函数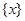 的定义域为
的定义域为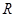 ,值域为
,值域为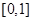 ;(2)方程
;(2)方程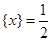 有无数个解;(3)函数
有无数个解;(3)函数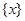 是周期函数;(4)函数
是周期函数;(4)函数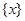 是增函数.其中正确命题的个数有( )
是增函数.其中正确命题的个数有( )| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com