
设椭圆C:![]() +y2=1(a>0)的两个焦点是F1(-c,0)和F2(c,0)(c>0),且椭圆C与圆x2+y2=c2有公共点.
+y2=1(a>0)的两个焦点是F1(-c,0)和F2(c,0)(c>0),且椭圆C与圆x2+y2=c2有公共点.
(Ⅰ)求a的取值范围;
(Ⅱ)若椭圆上的点到焦点的最短距离为![]() ,求椭圆的方程;
,求椭圆的方程;
(Ⅲ)对(2)中的椭圆C,直线l:y=kx+m(k≠0)与C交于不同的两点M、N,若线段MN的垂直平分线恒过点A(0,-1),求实数m的取值范围.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:甘肃省天水一中2010-2011学年高二第二阶段考试数学理科试题 题型:044
已知m>1,直线l:x-my-![]() =0,椭圆C:
=0,椭圆C:![]() +y2=1,F1F2分别为椭圆C的左、右焦点.
+y2=1,F1F2分别为椭圆C的左、右焦点.
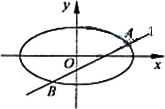
(Ⅰ)当直线l过右焦点F2时,求直线l的方程;
(Ⅱ)设直线l与椭圆C交于A,B两点,△AF1F2,△BF1F2的重心分别为G,H.若原点O在以线段GH为直径的圆内,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源:武汉市2007届高中毕业生四月调研测试题文理科数学试卷 题型:038
已知直线l:y=2x-![]() 与椭圆C:
与椭圆C:![]() +y2=1(a>1)交于P、Q两点,以PQ为直径的圆过椭圆C的右顶点A.
+y2=1(a>1)交于P、Q两点,以PQ为直径的圆过椭圆C的右顶点A.
(1)设PQ中点M(x0,y0),求证:x0<![]()
(2)求椭圆C的方程.
查看答案和解析>>
科目:高中数学 来源:2007届南通中学高三第二次调研、数学 题型:044
已知直线l∶y=2x-![]() 与椭圆C:
与椭圆C:![]() +y2=1(a>1)交于P、Q两点,以PQ为直径的圆过椭圆C的右顶点A.
+y2=1(a>1)交于P、Q两点,以PQ为直径的圆过椭圆C的右顶点A.
(1)设PQ中点M(x0,y0),求证:x0<![]()
(2)求椭圆C的方程.
查看答案和解析>>
科目:高中数学 来源:山东省实验中学2012届高三第四次诊断考试数学文科试题 题型:044
已知m>1,直线l:x-my-![]() =0,椭圆C:
=0,椭圆C:![]() +y2=1,F1,F2分别为椭圆C的左、右焦点.
+y2=1,F1,F2分别为椭圆C的左、右焦点.
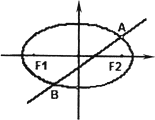
(Ⅰ)当直线l过右焦点F2时,求直线l的方程;
(Ⅱ)设直线l与椭圆C交于A,B两点,△AF1F2,△BF1F2的重心分别为G,H.若原点O在以线段GH为直径的圆内,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com