已知数列
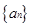
的前
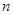
项和为
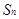
,且满足:
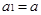
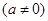
,
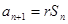
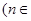
N
*,
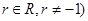
.
(1)求数列
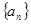
的通项公式;
(2)若存在
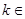
N
*,使得
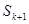
,
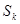
,
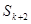
成等差数列,试判断:对于任意的
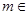
N
*,且
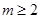
,
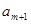
,
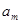
,
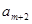
是否成等差数列,并证明你的结论.
(1)由已知
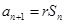
可得
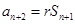
,两式相减可得
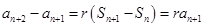
,
即
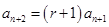
,又
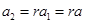
,
所以当r=0时,数列
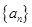
为a,0,0……,0,……;当
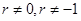
时,由已知
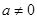
,所以
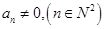
,于是由
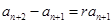
,可得
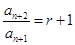
,所以
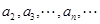
成等比数列,当
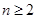
时,
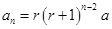
。
综上,数列
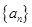
的通项公式为:
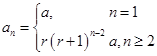
(6分)
(2)对于任意的
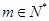
,且
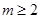
,
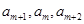
是否成等差数列,证明如下:
当r=0时,由(1),知
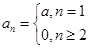
,
故对于任意的
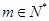
,且
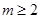
,
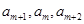
7成等差数列;
当
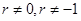
时,
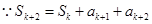
,
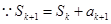
。
若存在
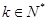
,使得
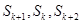
成等差数列,则
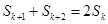
,
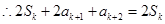
,即
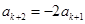
,
由(1),知
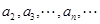
的公比
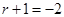
,
于是对于任意的
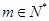
,且
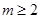
,
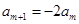
,从而
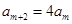
,
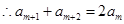
,即
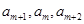
成等差数列。
综上,对于任意的
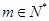
,且
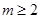
,
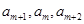
成等差数列。 (12分)
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
(2013·杭州模拟)已知数列{a
n}的前n项和S
n=-a
n-
 n-1
n-1+2(n∈N
*),数列{b
n}满足b
n=2
na
n.
(1)求证数列{b
n}是等差数列,并求数列{a
n}的通项公式.
(2)设数列
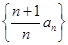
的前n项和为T
n,证明:n∈N
*且n≥3时,T
n>
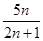
.
(3)设数列{c
n}满足a
n(c
n-3
n)=(-1)
n-1λn(λ为非零常数,n∈N
*),问是否存在整数λ,使得对任意n∈N
*,都有c
n+1>c
n.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知数列
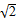
,
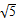
,2
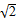
,
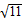
,…,则2
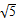
在这个数列中的项数为( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
(2013·宁波模拟)等差数列{a
n}中,已知a
1=-12,S
13=0,使得a
n>0的最小正整数n为( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
等差数列
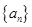
中,
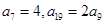
.
(1)求
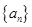
的通项公式;
(2)设
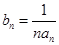
,求数列
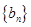
的前
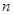
项和
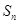
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
等差数列{a
n}中,S
15>0,S
16<0,则使a
n>0成立的n的最大值为( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
设数列
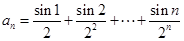
,则对任意正整数
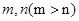
都成立的是( )
查看答案和解析>>

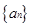 的前
的前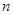 项和为
项和为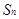 ,且满足:
,且满足: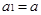
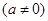 ,
,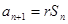
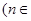 N*,
N*,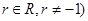 .
.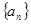 的通项公式;
的通项公式; 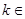 N*,使得
N*,使得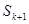 ,
,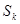 ,
,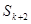 成等差数列,试判断:对于任意的
成等差数列,试判断:对于任意的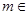 N*,且
N*,且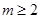 ,
,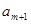 ,
,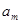 ,
,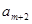 是否成等差数列,并证明你的结论.
是否成等差数列,并证明你的结论. 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 n-1+2(n∈N*),数列{bn}满足bn=2nan.
n-1+2(n∈N*),数列{bn}满足bn=2nan.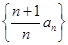 的前n项和为Tn,证明:n∈N*且n≥3时,Tn>
的前n项和为Tn,证明:n∈N*且n≥3时,Tn>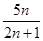 .
.