
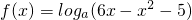 ,f(2)>0,则函数f(x)的减区间为________.
,f(2)>0,则函数f(x)的减区间为________.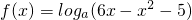 可看作由y=logat和t=-x2+6x-5复合而成的,
可看作由y=logat和t=-x2+6x-5复合而成的,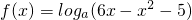 可看作由y=logat和t=-x2+6x-5复合而成的,y=logat单调递增,要求f(x)的减区间只需求出t=-x2+6x-5的减区间即可.
可看作由y=logat和t=-x2+6x-5复合而成的,y=logat单调递增,要求f(x)的减区间只需求出t=-x2+6x-5的减区间即可.

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源:2011-2012学年广东省广州六中高三(上)第三次月考数学试卷(文科)(解析版) 题型:选择题
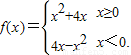 若f(2-a2)>f(a),则实数a的取值范围是( )
若f(2-a2)>f(a),则实数a的取值范围是( )查看答案和解析>>
科目:高中数学 来源:2013年上海市长宁区高考数学一模试卷(文科)(解析版) 题型:选择题
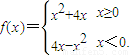 若f(2-a2)>f(a),则实数a的取值范围是( )
若f(2-a2)>f(a),则实数a的取值范围是( )查看答案和解析>>
科目:高中数学 来源:2011年高三数学(理科)一轮复习讲义:2.2 函数的单调性与最大(小)值(解析版) 题型:选择题
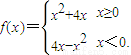 若f(2-a2)>f(a),则实数a的取值范围是( )
若f(2-a2)>f(a),则实数a的取值范围是( )查看答案和解析>>
科目:高中数学 来源:广东省高考数学一轮复习:3.7 函数的单调性(解析版) 题型:选择题
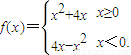 若f(2-a2)>f(a),则实数a的取值范围是( )
若f(2-a2)>f(a),则实数a的取值范围是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com