
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 无法确定 |
分析 由正弦定理可得a:b:c=3:5:7,进而可用b表示a,c,代入余弦定理化简可得cosC的值,结合C的范围即可得解C的值,从而得解.
解答 解:∵sinA:sinB:sinC=3:5:7,
∴由正弦定理可得:a:b:c=3:5:7,
∴a=$\frac{3b}{5}$,c=$\frac{7b}{5}$,
∴由余弦定理可得:cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{\frac{9{b}^{2}}{25}+{b}^{2}-\frac{49{b}^{2}}{25}}{2×\frac{3b}{5}×b}$=-$\frac{1}{2}$,
∵C∈(0,π),
∴C=$\frac{2π}{3}$.
故△ABC的形状是钝角三角形.
故选:C.
点评 本题主要考查了正弦定理,余弦定理在解三角形中的应用,考查了计算能力和转化思想,属于中档题.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (1,+∞) | C. | (0,1)∪(1,+∞) | D. | (-∞,0)∪(0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 想到“北上广”创业 | 不想到“北上广”创业 | 合计 | |
| 男性 | 10 | ||
| 女性 | 20 | ||
| 合计 | 100 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
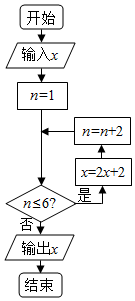
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{7}{30}$ | D. | $\frac{7}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
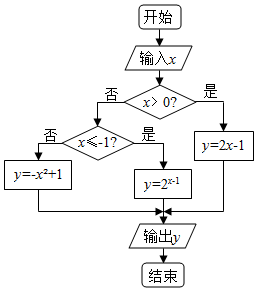
| A. | $\sqrt{2}$ | B. | $\frac{3}{4}$ | C. | -2 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com