解:(1)由题意可得对称轴-

=-1、且c=1、且a(x+1)
2+b(x+1)+c-[ax
2+bx+c]=x+

,
解得 a=

,且 b=1,且c=1,故有
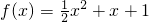
.
(2)由x∈[t,t+1],f(x)的对称轴为x=-1,且f(x)的最小值为h(t),
当t+1<-1,即t<-2时,函数f(x)在区间[t,t+1]上是减函数,h(t)=f(t+1)=

t
2+2t+

.
当 t≤-1≤t+1,即-2≤t≤-1时,h(t)=f(-1)=

,
当t>-1时,函数f(x)在区间[t,t+1]上是增函数,h(t)=f(t)=

t
2+t+1.
综上可得,
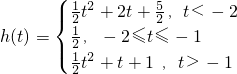
.
(3)由不等式
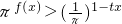
在t∈[-2,2]时恒成立,可得 f(x)>tx-1在t∈[-2,2]时恒成立,
即 m(x)=

x
2+(1-t)x+2>0 在t∈[-2,2]时恒成立.
根据二次函数的图象和性质可得
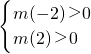
,解得-1<t<3,
故t的范围为(-1,3).
分析:(1)由题意可得对称轴-

=-1、且c=1、且a(x+1)
2+b(x+1)+c-[ax
2+bx+c]=x+

,解得a、b、c的值,可得函数f(x)的解析式.
(2)由f(x)的对称轴为x=-1,分当t+1<-1、当 t≤-1≤t+1、当t>-1三种情况,分别利用二次函数的性质,求得函数f(x)在区间[t,t+1]上的最小值h(t)=f(t)的解析式,综上可得结论.
(3)由不等式
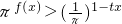
在t∈[-2,2]时恒成立,可得 f(x)>tx-1在t∈[-2,2]时恒成立,即 m(x)=

x
2+(1-t)x+2>0 在t∈[-2,2]时恒成立.根据二次函数的图象和性质可得
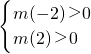
,由此解得t的范围.
点评:本题主要考查复合函数的单调性,指数不等式的解法,二次函数的性质,函数的恒成立问题,属于中档题

 .
.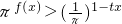 在t∈[-2,2]时恒成立,求实数x的取值范围.
在t∈[-2,2]时恒成立,求实数x的取值范围. =-1、且c=1、且a(x+1)2+b(x+1)+c-[ax2+bx+c]=x+
=-1、且c=1、且a(x+1)2+b(x+1)+c-[ax2+bx+c]=x+ ,
, ,且 b=1,且c=1,故有
,且 b=1,且c=1,故有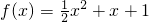 .
. t2+2t+
t2+2t+ .
. ,
, t2+t+1.
t2+t+1.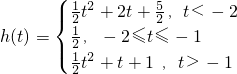 .
.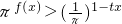 在t∈[-2,2]时恒成立,可得 f(x)>tx-1在t∈[-2,2]时恒成立,
在t∈[-2,2]时恒成立,可得 f(x)>tx-1在t∈[-2,2]时恒成立, x2+(1-t)x+2>0 在t∈[-2,2]时恒成立.
x2+(1-t)x+2>0 在t∈[-2,2]时恒成立.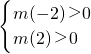 ,解得-1<t<3,
,解得-1<t<3, =-1、且c=1、且a(x+1)2+b(x+1)+c-[ax2+bx+c]=x+
=-1、且c=1、且a(x+1)2+b(x+1)+c-[ax2+bx+c]=x+ ,解得a、b、c的值,可得函数f(x)的解析式.
,解得a、b、c的值,可得函数f(x)的解析式.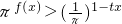 在t∈[-2,2]时恒成立,可得 f(x)>tx-1在t∈[-2,2]时恒成立,即 m(x)=
在t∈[-2,2]时恒成立,可得 f(x)>tx-1在t∈[-2,2]时恒成立,即 m(x)= x2+(1-t)x+2>0 在t∈[-2,2]时恒成立.根据二次函数的图象和性质可得
x2+(1-t)x+2>0 在t∈[-2,2]时恒成立.根据二次函数的图象和性质可得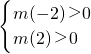 ,由此解得t的范围.
,由此解得t的范围.
