
已知集合![]() ,其中
,其中![]() ,
,![]() 表示
表示
![]() 的所有不同值的个数.
的所有不同值的个数.
(1)已知集合![]() ,
,![]() ,分别求
,分别求![]() ,
,![]() ;
;
(2)求![]() 的最小值.
的最小值.
解:(1)由2+4=6,2+6=8,2+8=10,4+6=10,4+8=12,6+8=14,
得l(P)=5
由2+4=6,2+8=10,2+16=18,4+8=12,4+16=20,8+16=24,
得l(Q)=6
(3)不妨设a1<a2<a3<…<an,可得
a1+a2<a1+a3<…<a1+an<a2+an<a3+an<…<an-1+an,
故ai+aj (1≤i<j≤n)中至少有2n-3个不同的数,即l(A)≥2n-3.
事实上,设a1,a2,a3,…,an成等差数列,考虑ai+aj (1≤i<j≤n),根据等差数列的性质,当i+j≤n时, ai+aj=a1+ai+j-1;当i+j>n时, ai+aj=ai+j-n+an;
因此每个和ai+aj(1≤i<j≤n)等于a1+ak(2≤k≤n)中的一个,或者等于al+an(2≤l≤n-1)中的一个.故对这样的集合A,l(A)=2n-3,所以l(A)的最小值为2n-3.


科目:高中数学 来源:2012-2013学年江苏省高三3月月考数学试卷(解析版) 题型:解答题
已知集合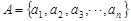 ,其中
,其中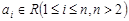 ,
,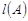 表示
表示
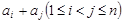 的所有不同值的个数.
的所有不同值的个数.
(1)已知集合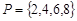 ,
,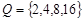 ,分别求
,分别求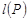 ,
,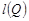 ;
;
(2)求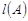 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知集合![]() ,其中
,其中![]() ,
,![]() 表示和
表示和![]() 中所有不同值的个数.
中所有不同值的个数.
(Ⅰ)设集合![]() ,
,![]() ,分别求
,分别求![]() 和
和![]() ;
;
(Ⅱ)若集合![]() ,求证:
,求证:![]() ;
;
(Ⅲ)![]() 是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由?
是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com