练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．函数f（x）=log2（3x-1）的零点是$\frac{2}{3}$．

    分析 直接利用函数为0，通过求解方程即可得到结果．

    解答 解：函数f（x）=log2（3x-1）的零点就是：log2（3x-1）=0的根，
    解得3x-1=1，即x=$\frac{2}{3}$．
    函数的零点为：$\frac{2}{3}$．
    故答案为：$\frac{2}{3}$．

    点评 本题考查函数的零点与方程根的关系，方程的解法，考查计算能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    12．已知椭圆N：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为e=$\frac{\sqrt{3}}{2}$，直线y=x+1被椭圆N截得的线段长为$\frac{8\sqrt{2}}{5}$，求椭圆N的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．下列函数存在极值的是②（填序号）
    ①y=$\frac{1}{x}$；②y=x-ex；③y=x3+x2+2x-3；④y=x3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知函数f（x）=logax（a＞0且a≠1）
    （1）当a=3时，求方程f（$\frac{27}{x}$）f（3x）=-5的解；
    （2）若f（3a-1）＞f（a），求实数a的取值范围；
    （3）当a=$\frac{1}{2}$时，设g（x）=f（x）-3x+4，求证：对任意λ＞0，都存在μ＞0，使得g（x）＜0对x∈（λμ，+∞）恒成立．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．下列说法不正确的是（　　）
    A．既有大小又有方向的量叫做向量
    B．不存在长度为零的向量
    C．如果两个向量相等，则两个向量的长度一定相同
    D．零向量可以和任何向量平行

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知函数f（x）=2cosx•sin（x+$\frac{π}{3}$）-$\sqrt{3}$sin2x+sinx•cosx．
    （1）当x∈[0，$\frac{π}{2}$]时，求f（x）的值域；
    （2）用五点法在图中作出y=f（x）在闭区间[-$\frac{π}{6}$，$\frac{5π}{6}$]上的简图；
    （3）说明f（x）的图象可由y=sinx的图象经过怎样的变化得到？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．已知等比数列{an}中，a5+a7=${∫}_{-2}^{2}$$\sqrt{4-{x}^{2}}$dx，则a6（a4+2a6+a8）的值为（　　）
    A．16π2B．4π2C．2π2D．π2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知空间向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$，$\overrightarrow{p}$，若存在实数组（x1，y1，z1）和（x2，y2，z2），满足$\overrightarrow{p}$=x1$\overrightarrow{a}$+y1$\overrightarrow{b}$+z1$\overrightarrow{c}$，$\overrightarrow{p}$=x2$\overrightarrow{a}$+y2$\overrightarrow{b}$+z2$\overrightarrow{c}$，且x1≠x2．试证明向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$共面．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

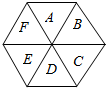    12．如图，一个正六边形分为6个区域A、B、C、D、E、F，现给这6个区域着色，要求同一区域染同一种颜色，相邻的两个区域不得使用同一颜色，现有红，黄，蓝，绿四种颜色可供选择，且A必须涂红色，则有多少种不同的着色方法？

    查看答案和解析>>

    同步练习册答案