
分析 首先写出二项展开式的通项,化简后按照要求确定字母的指数,得到特征项.
解答 解:二项式${({x-\frac{a}{{\sqrt{x}}}})^6}$(a>0)的展开式,通项为${C}_{6}^{k}{x}^{6-k}(-\frac{a}{\sqrt{x}})^{k}={C}_{6}^{k}(-a)^{k}{x}^{6-\frac{3}{2}k}$,
令6-$\frac{3}{2}k$=3,得到k=2,所以x3系数为A=${C}_{6}^{2}{a}^{2}$=15a2;
令6-$\frac{3}{2}$k=0,k=4,所以常数项为B=${C}_{6}^{4}(-a)^{4}$=15a4,
又B=4A,所以15a4=4×15a2,a>0,解得a=2;
故答案为:2
点评 本题考查了二项展开式的特征项的求法,关键是正确写出通项.


科目:高中数学 来源: 题型:解答题
 在(1+x+x2)n=D${\;}_{n}^{0}$+D${\;}_{n}^{1}$x+D${\;}_{n}^{2}$x2+…+D${\;}_{n}^{r}$xr+…D${\;}_{n}^{2n-1}$x2n-1+D${\;}_{n}^{2n}$x2n的展开式中,把D${\;}_{n}^{0}$,D${\;}_{n}^{1}$,D${\;}_{n}^{2}$,…,D${\;}_{n}^{2n}$叫做三项式系数.
在(1+x+x2)n=D${\;}_{n}^{0}$+D${\;}_{n}^{1}$x+D${\;}_{n}^{2}$x2+…+D${\;}_{n}^{r}$xr+…D${\;}_{n}^{2n-1}$x2n-1+D${\;}_{n}^{2n}$x2n的展开式中,把D${\;}_{n}^{0}$,D${\;}_{n}^{1}$,D${\;}_{n}^{2}$,…,D${\;}_{n}^{2n}$叫做三项式系数.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 相关指数R2为0.95的模型 | B. | 相关指数R2为0.81的模型 | ||
| C. | 相关指数R2为0.50的模型 | D. | 相关指数R2为0.32的模型 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 科幻片 | 文艺片 | 合计 | |
| 男 | 60 | 40 | 100 |
| 女 | 20 | 40 | 60 |
| 合计 | 80 | 80 | 160 |
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
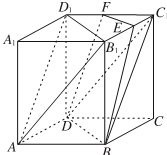 正方体ABCD-A1B1C1D1中,E,F分别为棱B1C1,C1D1的中点,
正方体ABCD-A1B1C1D1中,E,F分别为棱B1C1,C1D1的中点,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com