
 ,其中向量
,其中向量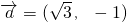 ,
,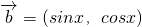 ,x∈R
,x∈R 的夹角;
的夹角;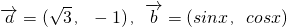
 =
=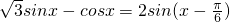
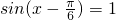
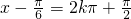 ,即
,即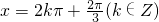 时,f(x)取得最大值
时,f(x)取得最大值
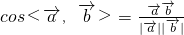 =
=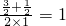
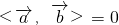
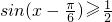
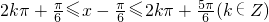
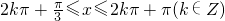
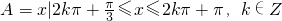
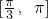
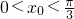
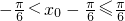
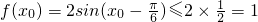


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
设函数![]() ,其中向量
,其中向量![]() ,
,![]() ,
,
![]() ,
,![]() 。
。
(1)求函数![]() 的最大值和最小正周期;
的最大值和最小正周期;
(2)将函数![]() 的图像按向量
的图像按向量![]() 平移,使平移后得到的图像关于坐标原点成中心对称,求长度最小的
平移,使平移后得到的图像关于坐标原点成中心对称,求长度最小的![]() 。
。
查看答案和解析>>
科目:高中数学 来源:2011年高三数学第一轮基础知识训练(22)(解析版) 题型:解答题
 ,其中向量
,其中向量 =(m,cos2x),
=(m,cos2x), =(1+sin2x,1),x∈R,且y=f(x)的图象经过点
=(1+sin2x,1),x∈R,且y=f(x)的图象经过点 .
.查看答案和解析>>
科目:高中数学 来源:2011-2012学年甘肃省高三上学期期末考试理科数学试卷 题型:解答题
(本题满分12分)设函数 ,其中向量
,其中向量 =(2cosx,1),
=(2cosx,1), =(cosx,
=(cosx,
 sin2x),x∈R.
sin2x),x∈R.
(1)若f(x)=1- 且x∈[-
且x∈[- ,
, ],求x;
],求x;
(2)若函数y=2sin2x的图象按向量 =(m,n)(|m|<
=(m,n)(|m|<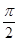 )平移后得到函数y=f(x)的图象,求实数m、n的值.
)平移后得到函数y=f(x)的图象,求实数m、n的值.
查看答案和解析>>
科目:高中数学 来源:2010年广东湛江市高一下学期期末考试数学卷 题型:解答题
(本小题满分12分)
设函数 ,其中向量
,其中向量 ,
, ,
, ,且
,且 的图象经过点
的图象经过点 .(1)求实数
.(1)求实数 的值;
的值;
(2)求函数 的最小值及此时
的最小值及此时 值的集合.
值的集合.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com