
【题目】设函数f(x)= ![]() ,若方程f(f(x))=a(a>0)恰有两个不相等的实根x1 , x2 , 则e
,若方程f(f(x))=a(a>0)恰有两个不相等的实根x1 , x2 , 则e ![]() e
e ![]() 的最大值为( )
的最大值为( )
A.![]()
B.2(ln2﹣1)
C.![]()
D.ln2﹣1
【答案】C
【解析】解:令g(x)=f(f(x))= ![]() ,
,
∵y=f(x)在(﹣∞,0)上单调递减,在[0,+∞)上单调递增,
∴g(x)=f(f(x))在(﹣∞,0)上单调递减,在[0,+∞)上单调递增.
做出g(x)=f(f(x))的函数图象如图所示:

∵方程f(f(x))=a(a>0)恰有两个不相等的实根x1,x2,
不妨设x1<x2,则x1≤﹣1,x2≥0,且f(x1)=f(x2),即x12=e ![]() .
.
∴e ![]() e
e ![]() =e
=e ![]() x12,
x12,
令h(x1)=e ![]() x12,则h′(x1)=e
x12,则h′(x1)=e ![]() (x12+2x1)=e
(x12+2x1)=e ![]() x1(x1+2),
x1(x1+2),
∴当x1<﹣2时,h′(x1)>0,当﹣2<x1<﹣1时,h′(x1)<0,
∴h(x1)在(﹣∞,﹣2)上单调递增,在(﹣2,﹣1)上单调递减,
∴当x1=﹣2时,h(x1)取得最大值h(﹣2)= ![]() .
.
故选C.


科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,
, ![]() .
.
(1)求函数 ![]() 的单调增区间;
的单调增区间;
(2)若 ![]() ,解不等式
,解不等式 ![]() ;
;
(3)若 ![]() ,且对任意
,且对任意 ![]() ,方程
,方程 ![]() 在
在 ![]() 总存在两不相等的实数根,求
总存在两不相等的实数根,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.
根据该折线图,下列结论错误的是( )
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系 ![]() 中,以坐标原点为极点,
中,以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系. 曲线
轴正半轴为极轴建立极坐标系. 曲线 ![]() 的极坐标方程为
的极坐标方程为 ![]() ,
, ![]() 为曲线
为曲线 ![]() 上异于极点的动点,点
上异于极点的动点,点 ![]() 在射线
在射线 ![]() 上,且
上,且 ![]() 成等比数列.
成等比数列.
(Ⅰ)求点 ![]() 的轨迹
的轨迹 ![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知 ![]() ,
, ![]() 是曲线
是曲线 ![]() 上的一点且横坐标为
上的一点且横坐标为 ![]() ,直线
,直线 ![]() 与
与 ![]() 交于
交于 ![]() 两点,试求
两点,试求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=(x﹣2)(ax+b)为偶函数,且在(0,+∞)单调递增,则f(2﹣x)>0的解集为( )
A.{x|x>2或x<﹣2}
B.{x|﹣2<x<2}
C.{x|x<0或x>4}
D.{x|0<x<4}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为对考生的月考成绩进行分析,某地区随机抽查了 ![]() 名考生的成绩,根据所得数据画了如下的样本频率分布直方图.
名考生的成绩,根据所得数据画了如下的样本频率分布直方图.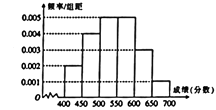
(1)求成绩在 ![]() 的频率;
的频率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析成绩与班级、学校等方面的关系,必须按成绩再从这 ![]() 人中用分层抽样方法抽取出
人中用分层抽样方法抽取出 ![]() 人作出进一步分析,则成绩在
人作出进一步分析,则成绩在 ![]() 的这段应抽多少人?
的这段应抽多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在等腰直角△ABO中,设 ![]() =
= ![]() ,
, ![]() =
= ![]() ,|
,| ![]() |=|
|=| ![]() |=1,C为AB上靠近A点的三等分点,过C作AB的垂线l,设P为垂线上任一点,
|=1,C为AB上靠近A点的三等分点,过C作AB的垂线l,设P为垂线上任一点, ![]() =
= ![]() ,则
,则 ![]() (
( ![]() ﹣
﹣ ![]() )=( )
)=( ) 
A.![]()
B.﹣ ![]()
C.﹣ ![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com