
【题目】如图,在多面体ABCPE中,平面PAC⊥平面ABC,AC⊥BC,PE∥BC,2PE=BC,M是线段AE的中点,N是线段PA上一点,且满足AN=![]() AP(0<
AP(0<![]() <1).
<1).
(Ⅰ)若![]() ,求证:MN⊥PC;
,求证:MN⊥PC;
(Ⅱ)是否存在![]() ,使得三棱锥M-ACN与三棱锥B-ACP的体积比为1:12?若存在,求出
,使得三棱锥M-ACN与三棱锥B-ACP的体积比为1:12?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

科目:高中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB=![]() ,AD=2,E,F为线段AB的三等分点,G、H为线段DC的三等分点.将长方形ABCD卷成以AD为母线的圆柱W的半个侧面,AB、CD分别为圆柱W上、下底面的直径.
,AD=2,E,F为线段AB的三等分点,G、H为线段DC的三等分点.将长方形ABCD卷成以AD为母线的圆柱W的半个侧面,AB、CD分别为圆柱W上、下底面的直径.

(Ⅰ)证明:平面ADHF⊥平面BCHF;
(Ⅱ)若P为DC的中点,求三棱锥H—AGP的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为庆祝国庆节,某中学团委组织了“歌颂祖国,爱我中华”知识竞赛,从参加考试的学生中抽出60名,将其成绩(成绩均为整数)分成[40,50),[50,60),…,[90,100)六组,并画出如图所示的部分频率分布直方图,观察图形,回答下列问题:
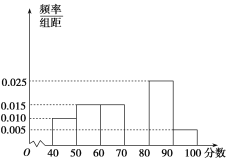
(1)求第四组的频率,并补全这个频率分布直方图;
(2)请根据频率分布直方图,估计样本的众数、中位数和平均数.(每组数据以区间的中点值为代表)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列![]() 中,若
中,若![]() (
(![]() ,
,![]() ,p为常数),则称
,p为常数),则称![]() 为“等方差数列”.下列是对“等方差数列”的判断,正确的是( )
为“等方差数列”.下列是对“等方差数列”的判断,正确的是( )
A.![]() 不是等方差数列;
不是等方差数列;
B.若![]() 既是等方差数列,又是等差数列,则该数列为常数列;
既是等方差数列,又是等差数列,则该数列为常数列;
C.已知数列![]() 是等方差数列,则数列
是等方差数列,则数列![]() 是等方差数列;
是等方差数列;
D.若![]() 是等方差数列,则
是等方差数列,则![]() (
(![]() ,k为常数)也是等方差数列.
,k为常数)也是等方差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F(2,0),动点P满足:点P到直线x=-1的距离比其到点F的距离小1.
(Ⅰ)求点P的轨迹C的方程;
(Ⅱ)过F作直线l垂直于x轴与曲线C交于A、B两点,Q是曲线C上异于A、B的一点,设曲线C在点A、B、Q处的切线分别为l1、l2、l3,切线l1、l2交于点R,切线l1、l3交于点S,切线l2、l3交于点T,若![]() RST的面积为6,求Q点的横坐标.
RST的面积为6,求Q点的横坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次社会实践活动中,某数学调研小组根据车间持续5个小时的生产情况画出了某种产品的总产量![]() (单位:千克)与时间
(单位:千克)与时间![]() (单位:小时)的函数图像,则以下关于该产品生产状况的正确判断是( ).
(单位:小时)的函数图像,则以下关于该产品生产状况的正确判断是( ).

A.在前三小时内,每小时的产量逐步增加
B.在前三小时内,每小时的产量逐步减少
C.最后一小时内的产量与第三小时内的产量相同
D.最后两小时内,该车间没有生产该产品
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中装有红球3个、白球2个、黑球1个,从中任取2个,则互斥而不对立的两个事件是![]()
![]()
A. 至少有一个白球;都是白球 B. 至少有一个白球;至少有一个红球
C. 至少有一个白球;红、黑球各一个 D. 恰有一个白球;一个白球一个黑球
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com