
分析 在①中,设AB=BC=CD=AD=2,取BD中点O,AC中点E,BC中点F,推导出△EFO是等边三角形,从而得到AB,CD所成的角为60°;在②中,由OA=OC=$\sqrt{2}$,且OA⊥OC,由此能得到△ADC为等边三角形;在③中,推导出BD⊥面AOC,从而AC⊥BD;在④中,推导出∠ABO是AB与平面BCD所成角,从而得到AB与平面BCD所成角为45°.
解答 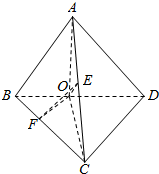 解:在①中:∵将正方形ABCD沿对角线BD折成直二面角,得到四面体A-BCD,
解:在①中:∵将正方形ABCD沿对角线BD折成直二面角,得到四面体A-BCD,
设AB=BC=CD=AD=2,
取BD中点O,AC中点E,BC中点F,连结AO,CO,OF,OE,EF,
则OA=OC=$\sqrt{2}$,且OA⊥OC,∴OE=$\frac{1}{2}AC$=1,
由三角形中位线定理得OF=$\frac{1}{2}CD=1$,EF=$\frac{1}{2}AB=1$,且OF∥CD,EF∥AB,
∴∠EFO是AB,CD所成的角,
∵OF=EF=OE=1,∴△EFO是等边三角形,∴∠EFO=60°,
∴AB,CD所成的角为60°,故①正确;
在②中:∵OA=OC=$\sqrt{2}$,且OA⊥OC,∴AC=$\sqrt{2+2}$=2,
∴AC=CD=AD=2,
∴②△ADC为等边三角形,故②正确;
在③中:∵AB=BC=CD=AD,O是BD中点,
∴AO⊥BD,CO⊥BD,又AO∩CO=O,∴BD⊥面AOC,
∵AC?面AOC,∴AC⊥BD,故③正确;
在④中:∵A-BD-C是直二面角,AO⊥BD,
∴AO⊥平面BDC,∴∠ABO是AB与平面BCD所成角,
∵AO=BO,∴∠ABO=45°,
∴AB与平面BCD所成角为45°,故④错误.
故答案为:①②③.
点评 本昰考查命题真假的判断,是中档题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=3,AD=2,PA=2,PD=2$\sqrt{2}$,∠PAB=60°.
如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=3,AD=2,PA=2,PD=2$\sqrt{2}$,∠PAB=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在三棱柱ABC-A1B1C1中,△ABC是边长为2的正三角形,侧面BB1C1C是矩形,D、E分别是线段BB1、AC1的中点.
在三棱柱ABC-A1B1C1中,△ABC是边长为2的正三角形,侧面BB1C1C是矩形,D、E分别是线段BB1、AC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图AB是圆O的直径,AF⊥AB,弦CD交AB、AF分别于E、F,交圆于点C.
如图AB是圆O的直径,AF⊥AB,弦CD交AB、AF分别于E、F,交圆于点C.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
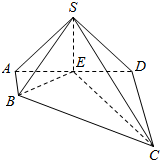 如图,在四棱锥S-ABCD中,AB⊥AD,AB∥CD,CD=3AB=3,平面SAD⊥平面ABCD,E是线段AD上一点,AE=ED=$\sqrt{3}$,SE⊥AD.
如图,在四棱锥S-ABCD中,AB⊥AD,AB∥CD,CD=3AB=3,平面SAD⊥平面ABCD,E是线段AD上一点,AE=ED=$\sqrt{3}$,SE⊥AD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,边长为2的正方体ABCD-A1B1C1D1中,B1C与BC1相交于点O.
如图,边长为2的正方体ABCD-A1B1C1D1中,B1C与BC1相交于点O.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com