
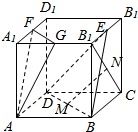
 如图,在正方体ABCD-A1B1C1D1中,E,F,G,M,N分别是B1C1,A1D1,A1B1,BD,B1C的中点,求证:
如图,在正方体ABCD-A1B1C1D1中,E,F,G,M,N分别是B1C1,A1D1,A1B1,BD,B1C的中点,求证:分析 (1)连接BC1,DC1,由已知推导出MN$\underset{∥}{=}$$\frac{1}{2}$DC1,由此能证明MN∥平面CDD1C1.
(2)连接EF,B1D1,推导出四边形ABEF为平行四边形,从而AF∥BE,由题意FG∥BD,由此能证明平面EBD∥平面FGA.
解答 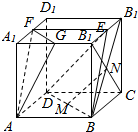 证明:(1)连接BC1,DC1,
证明:(1)连接BC1,DC1,
∵四边形BCC1B1为正方形,N为B1C的中点,
∴N在BC1上,且N为BC1的中点.
又∵M为BD的中点,∴MN$\underset{∥}{=}$$\frac{1}{2}$DC1.
又MN?平面CDD1C1,DC1?平面CDD1C1,
∴MN∥平面CDD1C1.(6分)
(2)连接EF,B1D1,则EF$\underset{∥}{=}$AB.
∴四边形ABEF为平行四边形,∴AF∥BE.
又由题意知FG∥B1D1,B1D1∥BD,∴FG∥BD.
又∵AF∩FG=F,BE∩BD=B,
∴平面EBD∥平面FGA.(12分)
点评 本题考查线面平行、面面平行的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:选择题
| A. | [-1,3] | B. | (-∞,-1)∪(3,+∞) | C. | (-1,3) | D. | (-∞,-1]∪[3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,4] | B. | [2,4) | C. | [2,4] | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知抛物线C:y2=2px(p>0)上的点(2,a)到焦点F的距离为3.
已知抛物线C:y2=2px(p>0)上的点(2,a)到焦点F的距离为3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com