
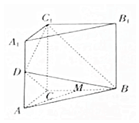
 如图,在直三棱柱ABC-A1B1C1中,D,M分别是AA1,BC的中点,∠CDC1=90°,在△ABC中,AB=2AC,∠BAC=60°.
如图,在直三棱柱ABC-A1B1C1中,D,M分别是AA1,BC的中点,∠CDC1=90°,在△ABC中,AB=2AC,∠BAC=60°.分析 (1)取BC1的中点N,连接DN,MN,证明:四边形ADNM为平行四边形,可得DN∥AM,即可证明AM∥平面BDC1;
(2)证明:DC1⊥BC,DC1⊥DC,且DC∩BC=C,即可证明DC1⊥平面BDC.
解答 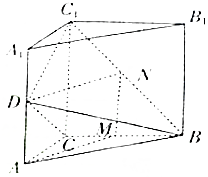 证明:(1)取BC1的中点N,连接DN,MN,
证明:(1)取BC1的中点N,连接DN,MN,
则$MN∥\frac{1}{2}C{C_1}$且$MN=\frac{1}{2}C{C_1}$.
又$AD∥\frac{1}{2}C{C_1}$且$AD=\frac{1}{2}C{C_1}$,
∴AD∥MN,且AD=MN,
∴四边形ADNM为平行四边形,
∴DN∥AM.
又DN?平面BDC1,AM?平面BDC1,
∴AM∥平面BDC1.
(2)由题设AC=1,则AB=2,
由余弦定理,得$BC=\sqrt{3}$.
由勾股定理,得∠ACB=90°,BC⊥AC1.
又∵BC⊥CC1,且CC1∩AC=C,
∴BC⊥平面ACC1A1.
又DC1?平面ACC1A1,∴DC1⊥BC.
又DC1⊥DC,且DC∩BC=C,
∴DC1⊥平面BDC.
点评 本小题主要考查空间线面关系等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}+\frac{1}{2}i$ | B. | $\frac{1}{2}+i$ | C. | $\frac{1}{4}-\frac{1}{2}i$ | D. | $\frac{1}{2}-i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,4,5} | B. | {1,2,4,5} | C. | {2,5} | D. | {0,2,3,4,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
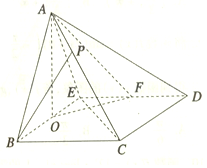 在四棱锥A-BCDE中,底面BCDE为菱形,侧面ABE为等边三角形,且侧面ABE⊥底面BCDE,O,F分别为BE,DE的中点,点P在AC上,且AP=$\frac{1}{3}$AC.
在四棱锥A-BCDE中,底面BCDE为菱形,侧面ABE为等边三角形,且侧面ABE⊥底面BCDE,O,F分别为BE,DE的中点,点P在AC上,且AP=$\frac{1}{3}$AC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
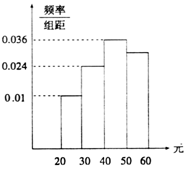 为了倡导人民群众健康的生活方式,某社区服务中心通过网站对岁的社区居民随机抽取n人进行了调查,得到如下各年龄段人数频率分布直方图,若该公司决定在各年龄段用分层抽样抽取50名观众进行奖励,则年龄段[50,60]的获奖人数为( )
为了倡导人民群众健康的生活方式,某社区服务中心通过网站对岁的社区居民随机抽取n人进行了调查,得到如下各年龄段人数频率分布直方图,若该公司决定在各年龄段用分层抽样抽取50名观众进行奖励,则年龄段[50,60]的获奖人数为( )| A. | 10 | B. | 12 | C. | 15 | D. | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com