练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数.

    (Ⅰ)若存在使得成立,求实数的取值范围；

    (Ⅱ)求证：当时,在(1)的条件下, 成立．

    【答案】(Ⅰ) ； (Ⅱ)见解析．

    【解析】试题分析: (1)构造函数 ,求出 在 的最小值,从而得到实数的取值范围；（2）设 ，求出 的单调性，得出结论.

    (Ⅰ)原题即为存在,使得,

    ∴,

    令,则.

    令,解得.

    ∵当时, ,∴为减函数,

    当时, ，∴为增函数,

    ∴,∴.

    ∴的取值范围为.

    (Ⅱ)原不等式可化为,

    令,则,

    ,

    ∵,由(Ⅰ)可知, ,

    则,

    ∴在上单调递增,

    ∴当时, .

    ∴成立.

    即当时, 成立.

    点睛: 本题主要考查了导数在求函数的单调性，函数的最值上的应用，属于中档题.考查学生灵活运用导数工具去分析、解决问题的能力,综合考查学生的逻辑思维能力、运算求解能力和推理论证能力以及等价转换的解题思想.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知过抛物线y2＝2px（p>0）的焦点，斜率为2的直线交抛物线于A（x1，y1），B（x2，y2）（x1<x2）两点，且|AB|＝9．

    （1）求该抛物线的方程．

    （2）O为坐标原点，C为抛物线上一点，若，求λ的值

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在中, 成等差数列是的( )

    A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的左、右焦点分别为,离心率为,点是椭圆上任意一点, 的周长为.

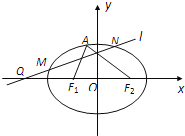
    (Ⅰ)求椭圆的方程；

    (Ⅱ)过点 (-4,0)任作一动直线交椭圆于两点,记,若在线段上取一点,使得,则当直线转动时,点在某一定直线上运动,求该定直线的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】中心在原点，焦点在x轴上的一椭圆与一双曲线有共同的焦点F1，F2，且|F1F2|＝，椭圆的长半轴与双曲线实半轴之差为4，离心率之比为3∶7.

    （1）求这两曲线的方程；

    （2）若P为这两曲线的一个交点，求cos∠F1PF2的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示, 是边长为3的正方形, 平面与平面所成角为.

    (Ⅰ)求证： 平面；

    (Ⅱ)设点是线段上一个动点,试确定点的位置,使得平面,并证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2017年9月16日05时，第19号台风“杜苏芮”的中心位于甲地，它以每小时30千米的速度向西偏北的方向移动，距台风中心千米以内的地区都将受到影响，若16日08时到17日08时，距甲地正西方向900千米的乙地恰好受台风影响，则和的值分别为（附： ）（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）当时，判断的单调性；

    （2）若在上为单调增函数，求实数 的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，椭圆的离心率为，顶点为，且．

    （1）求椭圆的方程；

    （2）是椭圆上除顶点外的任意点，直线交轴于点，直线交于点．设的斜率为， 的斜率为，试问是否为定值？并说明理由．

    查看答案和解析>>

    同步练习册答案