
【题目】北京联合张家口获得2022年第24届冬奥会举办权,我国各地掀起了发展冰雪运动的热潮,现对某高中的学生对于冰雪运动是否感兴趣进行调查,该高中男生人数是女生的1.2倍,按照分层抽样的方法,从中抽取110人,调查高中生“是否对冰雪运动感兴趣”得到如下列联表:
感兴趣 | 不感兴趣 | 合计 | |
男生 | 40 | ||
女生 | 30 | ||
合计 | 110 |
(1)补充完成上述![]() 列联表;
列联表;
(2)是否有99%的把握认为是否喜爱冰雪运动与性别有关.
附:![]() (其中
(其中![]() ).
).
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
科目:高中数学 来源: 题型:
【题目】已知![]() ,
, ![]() ,
, ![]() ,
, ![]() .给出以下三个命题:
.给出以下三个命题:
①分别过点![]() ,
, ![]() ,作
,作![]() 的不同于
的不同于![]() 轴的切线,两切线相交于点
轴的切线,两切线相交于点![]() ,则点
,则点![]() 的轨迹为椭圆的一部分;
的轨迹为椭圆的一部分;
②若![]() ,
, ![]() 相切于点
相切于点![]() ,则点
,则点![]() 的轨迹恒在定圆上;
的轨迹恒在定圆上;
③若![]() ,
, ![]() 相离,且
相离,且![]() ,则与
,则与![]() ,
, ![]() 都外切的圆的圆心在定椭圆上.
都外切的圆的圆心在定椭圆上.
则以上命题正确的是( )
A. ①② B. ①③ C. ②③ D. ①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四面体ABCD中,△ABC是等边三角形,平面ABC⊥平面ABD,点M为棱AB的中点,AB=2,AD=![]() ,∠BAD=90°.
,∠BAD=90°.
(Ⅰ)求证:AD⊥BC;
(Ⅱ)求异面直线BC与MD所成角的余弦值;
(Ⅲ)求直线CD与平面ABD所成角的正弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】唐代诗人李欣的是![]() 古从军行
古从军行![]() 开头两句说“百日登山望烽火,黄昏饮马傍交河”诗中隐含着一个有缺的数学故事“将军饮马”的问题,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回到军营,怎样走才能使总路程最短?在平面直角坐标系中,设军营所在区域为
开头两句说“百日登山望烽火,黄昏饮马傍交河”诗中隐含着一个有缺的数学故事“将军饮马”的问题,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回到军营,怎样走才能使总路程最短?在平面直角坐标系中,设军营所在区域为![]() ,若将军从
,若将军从![]() 出发,河岸线所在直线方程
出发,河岸线所在直线方程![]() ,并假定将军只要到达军营所在区域即回到军营,则“将军饮马”的最短总路程为( )
,并假定将军只要到达军营所在区域即回到军营,则“将军饮马”的最短总路程为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某种植物每日平均增长高度![]() (单位:
(单位:![]() )与每日光照时间
)与每日光照时间![]() (单位:
(单位:![]() )之间的关系有如下一组数据:
)之间的关系有如下一组数据:
| 6 | 7 | 8 | 9 | 10 |
| 3.5 | 5.2 | 7 | 8.6 | 10.7 |
(1)求![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)计算相关指数![]() 的值,并说明回归模型拟合程度的好坏;
的值,并说明回归模型拟合程度的好坏;
(3)若某天光照时间为8.5小时, 预测该天这种植物的平均增长高度(结果精确到0.1)
参考公式及数据: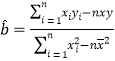 ,
,![]() ,
,![]() ,
,![]()
![]() ,
,,
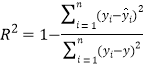
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=xln x,g(x)=x3+ax2-x+2.
(1)如果函数g(x)在区间![]() 上单调递减,求实数a的取值范围;
上单调递减,求实数a的取值范围;
(2)对任意x∈(0,+∞),2f(x)≤g′(x)+2恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某课题小组共10人,已知该小组外出参加交流活动次数为1,2,3的人数分别为3,3, 4,现从这10人中随机选出2人作为该组代表参加座谈会.
(1)记“选出2人外出参加交流活动次数之和为4”为事件A,求事件A发生的概率;
(2)设X为选出2人参加交流活动次数之差的绝对值,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下四个说法:
①残差点分布的带状区域的宽度越窄相关指数越小
②在刻画回归模型的拟合效果时,相关指数![]() 的值越大,说明拟合的效果越好;
的值越大,说明拟合的效果越好;
③在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加一个单位时,预报变量
每增加一个单位时,预报变量![]() 平均增加
平均增加![]() 个单位;
个单位;
④对分类变量![]() 与
与![]() ,若它们的随机变量
,若它们的随机变量![]() 的观测值
的观测值![]() 越小,则判断“
越小,则判断“![]() 与
与![]() 有关系”的把握程度越大.
有关系”的把握程度越大.
其中正确的说法是![]()
A. ①④B. ②④C. ①③D. ②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com