
 对称,又f(x)在区间[0,
对称,又f(x)在区间[0, ]上是单调函数.
]上是单调函数. 个单位后,得到函数y=g(x)的图象.
个单位后,得到函数y=g(x)的图象.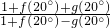 +4f(10°);
+4f(10°); ]上有唯一实根,求实数m的取值范围.
]上有唯一实根,求实数m的取值范围. .…(1分)
.…(1分) )=sinωx.…(2分)
)=sinωx.…(2分) 对称,且ω>0,得
对称,且ω>0,得 =kπ+
=kπ+ (k∈N),解得ω=4k+2(k∈N).①…(3分)
(k∈N),解得ω=4k+2(k∈N).①…(3分)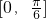 上是单调函数,所以0≤ω•x≤ω•
上是单调函数,所以0≤ω•x≤ω• ≤
≤ ,
, )=sin(2x-
)=sin(2x- )=-cos2x.…(6分)
)=-cos2x.…(6分)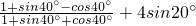
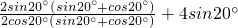
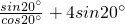 …(7分)
…(7分)
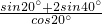 …(8分)
…(8分)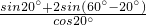 …(9分)
…(9分)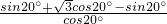
 .…(10分)
.…(10分) sin(2x+
sin(2x+ ).…(11分)
).…(11分) sin(2x+
sin(2x+ )在区间
)在区间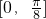 上单调递增,在区间
上单调递增,在区间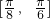 上单调递减.…(12分)
上单调递减.…(12分) 时,f(x)-g(x)=
时,f(x)-g(x)= ;
; 时,f(x)-g(x)=
时,f(x)-g(x)= .…(13分)
.…(13分) 或1≤m<
或1≤m< .…(14分)
.…(14分) 个单位后,得到函数y=g(x)的图象即可得到表达式,
个单位后,得到函数y=g(x)的图象即可得到表达式,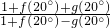 +4f(10°),利用二倍角公式,化简整理可求结果;
+4f(10°),利用二倍角公式,化简整理可求结果; ]上有唯一实根,求出实数m的取值范围.
]上有唯一实根,求出实数m的取值范围.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:
| 1-x | 1+x |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| π |
| 3 |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com