
【题目】下列命题:①“![]() ”是“存在
”是“存在![]() ,使得
,使得![]() 成立”的充分不必要条件;②“
成立”的充分不必要条件;②“![]() ”是“存在
”是“存在![]() ,使得
,使得![]() 成立”的必要条件;③“
成立”的必要条件;③“![]() ”是“不等式
”是“不等式![]() 对一切
对一切![]() 恒成立”的充要条件. 其中所以真命题的序号是
恒成立”的充要条件. 其中所以真命题的序号是
A.③B.②③C.①②D.①③
科目:高中数学 来源: 题型:
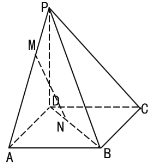
【题目】如图,四棱锥P-ABCD底面为正方形,PD⊥平面ABCD,PD=AD,点M为线段PA上任意一点(不含端点),点N在线段BD上,且PM=DN.
(1)求证:直线MN∥平面PCD.
(2)若点M为线段PA的中点,求直线PB与平面AMN所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx+![]() ﹣1,a∈R.
﹣1,a∈R.
(1)当a>0时,若函数f(x)在区间[1,3]上的最小值为![]() ,求a的值;
,求a的值;
(2)讨论函数g(x)=f′(x)﹣![]() 零点的个数.
零点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,半径为2的![]() 切直线MN于点P,射线PK从PN出发绕点P逆时针方向旋转到PM,旋转过程中,PK交
切直线MN于点P,射线PK从PN出发绕点P逆时针方向旋转到PM,旋转过程中,PK交![]() 于点Q,设
于点Q,设![]() 为x,弓形PmQ的面积为
为x,弓形PmQ的面积为![]() ,那么
,那么![]() 的图象大致是
的图象大致是![]()
![]()

A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 个正数
个正数![]() 依次围成一个圆圈,其中
依次围成一个圆圈,其中![]()
![]() 是公差为
是公差为![]() 的等差数列,而
的等差数列,而![]() 是公比为
是公比为![]() 的等比数列.
的等比数列.
(1)若![]() ,求数列
,求数列![]() 的所有项的和
的所有项的和![]() ;
;
(2)若![]() ,求
,求![]() 的最大值;
的最大值;
(3)当![]() 时是否存在正整数
时是否存在正整数![]() ,满足
,满足![]() ?若存在,求出
?若存在,求出![]() 值;若不存在,请说明理由.
值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在边长为4的菱形![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,将
,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使
的位置,使![]() ,如图2.
,如图2.

(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)判断在线段![]() 上是否存在一点
上是否存在一点![]() ,使平面
,使平面![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将![]() 个不同的红球和
个不同的红球和![]() 个不同的白球,放入同一个袋中,现从中取出
个不同的白球,放入同一个袋中,现从中取出![]() 个球.
个球.
(1)若取出的红球的个数不少于白球的个数,则有多少种不同的取法;
(2)取出一个红球记![]() 分,取出一个白球记
分,取出一个白球记![]() 分,若取出
分,若取出![]() 个球的总分不少于
个球的总分不少于![]() 分,则有多少种不同的取法;
分,则有多少种不同的取法;
(3)若将取出的![]() 个球放入一箱子中,记“从箱子中任意取出
个球放入一箱子中,记“从箱子中任意取出![]() 个球,然后放回箱子中”为一次操作,如果操作三次,求恰有一次取到
个球,然后放回箱子中”为一次操作,如果操作三次,求恰有一次取到![]() 个红球并且恰有一次取到
个红球并且恰有一次取到![]() 个白球的概率.
个白球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com