
【题目】 如图,△ABC的角平分线AD的延长线交它的外接圆于点![]()
(Ⅰ)证明:△ABE∽△ADC;
(Ⅱ)若△ABC的面积![]() ,求
,求![]() 的大小.
的大小.

【答案】(Ⅰ)证明见解析;(Ⅱ)![]() .
.
【解析】
(Ⅰ)先证明∠BAE=∠CAD,∠AEB=∠ACD,利用相似三角形的判定定理可得结论;(Ⅱ)利用三角形相似可得AB·AC=AD·AE,结合△ABC的面积![]() ,可得sin∠BAC=1,从而可得结果.
,可得sin∠BAC=1,从而可得结果.
由已知条件,可得∠BAE=∠CAD.
因为∠AEB与∠ACB是同弧上的圆周角,
所以∠AEB=∠ACD.
故△ABE∽△ADC.
(Ⅱ)因为△ABE∽△ADC,所以![]() ,
,
即AB·AC=AD·AE.
又S=![]() AB·AC·sin∠BAC,且S=
AB·AC·sin∠BAC,且S=![]() AD·AE,
AD·AE,
故AB·AC·sin∠BAC=AD·AE.
则sin∠BAC=1,又∠BAC为三角形内角,所以∠BAC=90°.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:高中数学 来源: 题型:
【题目】下列有关命题的说法正确的是( )
A. ![]() ,使得
,使得![]() 成立.
成立.
B. 命题![]() :任意
:任意![]() ,都有
,都有![]() ,则
,则![]() :存在
:存在![]() ,使得
,使得![]() .
.
C. 命题“若![]() 且
且![]() ,则
,则![]() 且
且![]() ”的逆命题为真命题.
”的逆命题为真命题.
D. 若数列![]() 是等比数列,
是等比数列,![]() 则
则![]() 是
是![]() 的必要不充分条件.
的必要不充分条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着“互联网+交通”模式的迅猛发展,“共享助力单车”在很多城市相继出现.某“共享助力单车”运营公司为了解某地区用户对该公司所提供的服务的满意度,随机调查了100名用户,得到用户的满意度评分(满分10分),现将评分分为5组,如下表:
组别 | 一 | 二 | 三 | 四 | 五 |
满意度评分 | [0,2) | [2,4) | [4,6) | [6,8) | [8,10] |
频数 | 5 | 10 | a | 32 | 16 |
频率 | 0.05 | b | 0.37 | c | 0.16 |
(1)求表格中的a,b,c的值;
(2)估计用户的满意度评分的平均数;
(3)若从这100名用户中随机抽取25人,估计满意度评分低于6分的人数为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方形![]() 中,点
中,点![]() 是
是![]() 的中点,点
的中点,点![]() 是
是![]() 的中点,将
的中点,将![]() 分别沿
分别沿![]() 折起,使
折起,使![]() 两点重合于
两点重合于![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
(2)点![]() 是
是![]() 上一点,若
上一点,若![]() 平面
平面![]() ,则
,则![]() 为何值?并说明理由.
为何值?并说明理由.
(3)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.


查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在[29.94,30.06)的零件为优质品.从两个分厂生产的零件中各抽出了500件,量其内径尺寸,得结果如下表:
甲厂:
分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.98,30.02) | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
频数 | 12 | 63 | 86 | 182 | 92 | 61 | 4 |
乙厂:
分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.98,30.02) | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
频数 | 29 | 71 | 85 | 159 | 76 | 62 | 18 |
(1)试分别估计两个分厂生产的零件的优质品率;
(2)由以上统计数据填下面![]() 列联表,并问是否有
列联表,并问是否有![]() 的把握认为“两个分厂生产的零件的质量有差异”.
的把握认为“两个分厂生产的零件的质量有差异”.
甲 厂 | 乙 厂 | 合计 | |
优质品 | |||
非优质品 | |||
合计 |
附: 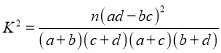
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 如图,在四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形,![]() 为等边三角形,平面
为等边三角形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,

(Ⅰ)设![]() 分别为
分别为![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(Ⅱ)求证:![]() 平面
平面![]() ;
;
(Ⅲ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com