已知数列{an}中,a0=2,a1=3,a2=6,且对n≥3时,有an=(n+4)an-1-4nan-2+(4n-8)an-3.
(Ⅰ)设数列{bn}满足bn=an-nan-1,n∈N*,证明数列{bn+1-2bn}为等比数列,并求数列{bn}的通项公式;
(Ⅱ)记n×(n-1)×…×2×1=n!,求数列{nan}的前n项和Sn.
解:(Ⅰ) 证明:由条件,得a
n-na
n-1=4[a
n-1-(n-1)a
n-2]-4[a
n-2-(n-2)a
n-3],
则a
n+1-(n+1)a
n=4[a
n-na
n-1]-4[a
n-1-(n-1)a
n-2].…2分
即b
n+1=4b
n-4b
n-1.又b
1=1,b
2=0,所以b
n+1-2b
n=2(b
n-2b
n-1),b
2-2b
1=-2≠0.
所以{b
n+1-2b
n}是首项为-2,公比为2的等比数列. …4分b
2-2b
1=-2,所以b
n+1-2b
n=2
n-1(b
2-2b
1)=-2
n.
两边同除以2
n+1,可得

.…6分
于是
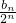
为以

首项,-

为公差的等差数列.
所以

.…8分
(Ⅱ)a
n-2
n=na
n-1-n2
n-1=n(a
n-1-2
n-1),令c
n=a
n-2
n,则c
n=nc
n-1.
而c
1=1,∴c
n=n(n-1)•…•2•1•c
1=n(n-1)•…•2•1.
∴a
n=n(n-1)•…•2•1+2
n. …12分na
n=n•n•(n-1)•…•2•1+n2
n=(n+1)!-n!+n•2
n,
∴S
n=(2!-1!)+(3!-2!)+…+(n+1)!-n!+(1×2+2×2
2+…+n×2
n).…14分
令T
n=1×2+2×2
2+…+n×2
n,①
则2T
n=1×2
2+2×2
3+…+(n-1)×2
n+n×2
n+1.②
①-②,得-T
n=2+2
2+…+2
n-n×2
n+1,T
n=(n-1)2
n+1+2.
∴

.…16分.
分析:(Ⅰ)由条件,得a
n-na
n-1=4[a
n-1-(n-1)a
n-2]-4[a
n-2-(n-2)a
n-3],进而再写一式a
n+1-(n+1)a
n=4[a
n-na
n-1]-4[a
n-1-(n-1)a
n-2].代入化简得b
n+1=4b
n-4b
n-1.构建数列{b
n+1-2b
n},从而可证明其是首项为-2,公比为2的等比数列.由此可求数列{b
n}的通项公式;
(Ⅱ)易得na
n=n•n•(n-1)•…•2•1+n2
n=(n+1)!-n!+n•2
n,从而S
n=(2!-1!)+(3!-2!)+…+(n+1)!-n!+(1×2+2×2
2+…+n×2
n),同乘公比,错位相减可求.
点评:本题以数列递推式为载体,考查数列的通项及求和问题,掌握通解通法是关键.应学会构造法求数列的通项.

 .…6分
.…6分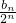 为以
为以 首项,-
首项,- 为公差的等差数列.
为公差的等差数列. .…8分
.…8分 .…16分.
.…16分.
