
分析 根据题意,分分4步进行分析:①、先分析身高最高的同学,由于其只能在中间位置,可得其有1种情况,②、再分析身高排第4高的同学,由于其必须与身高最高的同学相邻,易得其站法数目,③、在高排第5、6、7、8、9高的5个同学中,任选3个,按身高由高到低的顺序,排在身高排第4高的同学一边,④.剩余的4名同学,按身高由高到低的顺序,排在身高最高的同学的另一边,由组合数公式易得其站法数目,由分步计数原理计算可得答案.
解答 解:根据题意,分4步进行分析:
①、身高最高的同学只能在中间位置,有1种情况,
②、身高排第4高的同学与身高最高的同学相邻,可以在身高最高的同学的左边或右边,有2种情况,
③、在高排第5、6、7、8、9高的5个同学中,任选3个,按身高由高到低的顺序,排在身高排第4高的同学一边,有C53=10种情况,
④.剩余的4名同学,按身高由高到低的顺序,排在身高最高的同学的另一边,有1种情况,
则共有1×2×10×1=20种不同的站位顺序;
故答案为:20.
点评 本题考查排列、组合的综合应用,涉及分步计数原理的应用,注意优先分析受到限制的元素.


科目:高中数学 来源: 题型:选择题
| A. | 第一种 | B. | 第二种 | C. | 两种一样 | D. | 无法判断 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,4,5} | B. | {1,2,4,5} | C. | {2,5} | D. | {0,2,3,4,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
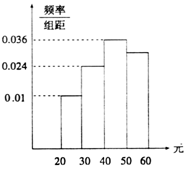 为了倡导人民群众健康的生活方式,某社区服务中心通过网站对岁的社区居民随机抽取n人进行了调查,得到如下各年龄段人数频率分布直方图,若该公司决定在各年龄段用分层抽样抽取50名观众进行奖励,则年龄段[50,60]的获奖人数为( )
为了倡导人民群众健康的生活方式,某社区服务中心通过网站对岁的社区居民随机抽取n人进行了调查,得到如下各年龄段人数频率分布直方图,若该公司决定在各年龄段用分层抽样抽取50名观众进行奖励,则年龄段[50,60]的获奖人数为( )| A. | 10 | B. | 12 | C. | 15 | D. | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{b-a}{2}$ | B. | $\frac{b+a}{2}$ | C. | $\frac{1-b}{2}$ | D. | $\frac{1-a}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
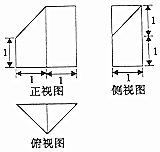
| A. | $\frac{9}{2}$+4$\sqrt{2}$ | B. | 5$+4\sqrt{2}$ | C. | 6$+4\sqrt{2}$ | D. | $\frac{13}{2}$$+4\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com