
【题目】如图1,在直角梯形ABCD中,AD∥BC,∠BAD= ![]() ,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到图2中△A1BE的位置,得到四棱锥A1﹣BCDE.
,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到图2中△A1BE的位置,得到四棱锥A1﹣BCDE. 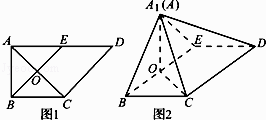
(Ⅰ) 证明:CD⊥平面A1OC;
(Ⅱ) 若平面A1BE⊥平面BCDE,求平面A1BC与平面A1CD夹角(锐角)的余弦值.
【答案】证明:(Ⅰ)在图1中,∵AB=BC=1,AD=2,E是AD的中点,∠BAD= ![]() , ∴BE⊥AC,
, ∴BE⊥AC,
即在图2中,BE⊥OA1 , BE⊥OC,
则BE⊥平面A1OC;
∵CD∥BE,
∴CD⊥平面A1OC.
解:(Ⅱ)若平面A1BE⊥平面BCDE,
由(Ⅰ)知BE⊥OA1 , BE⊥OC,
∴∠A1OC为二面角A1﹣BE﹣C的平面角,
∴∠A1OC= ![]() ,
,
如图,建立空间坐标系,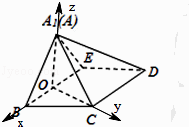
∵A1B=A1E=BC=ED=1.BC∥ED
∴B( ![]() ,0,0),E(﹣
,0,0),E(﹣ ![]() ,0,0),A1(0,0,
,0,0),A1(0,0, ![]() ),C(0,
),C(0, ![]() ,0),
,0),![]() =(﹣
=(﹣ ![]() ,
, ![]() ,0),
,0), ![]() =(0,
=(0, ![]() ,﹣
,﹣ ![]() ),
), ![]() =
= ![]() =(﹣
=(﹣ ![]() ,0,0),
,0,0),
设平面A1BC的法向量为 ![]() =(x,y,z),平面A1CD的法向量为
=(x,y,z),平面A1CD的法向量为 ![]() =(a,b,c),
=(a,b,c),
则 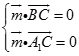 ,得
,得 ![]() ,令x=1,则y=1,z=1,即
,令x=1,则y=1,z=1,即 ![]() =(1,1,1),
=(1,1,1),
由 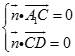 ,得
,得 ![]() ,取b=1,得
,取b=1,得 ![]() =(0,1,1),
=(0,1,1),
则cos< ![]() ,
, ![]() >=
>= ![]() =
= ![]() =
= ![]() ,
,
∴平面A1BC与平面A1CD夹角(锐角)的余弦值为 ![]() .
.
【解析】(Ⅰ)根据线面垂直的判定定理即可证明:CD⊥平面A1OC;(Ⅱ)若平面A1BE⊥平面BCDE,建立空间坐标系,利用向量法即可求平面A1BC与平面A1CD夹角的余弦值.
【考点精析】认真审题,首先需要了解直线与平面垂直的判定(一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知α∈[ ![]() ,
, ![]() ],β∈[﹣
],β∈[﹣ ![]() ,0],且(α﹣
,0],且(α﹣ ![]() )3﹣sinα﹣2=0,8β3+2cos2β+1=0,则sin(
)3﹣sinα﹣2=0,8β3+2cos2β+1=0,则sin( ![]() +β)的值为( )
+β)的值为( )
A.0
B.![]()
C.![]()
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在班级的演讲比赛中,将甲、乙两名同学的得分情况制成如图所示的茎叶图.记甲、乙两名同学所得分数的平均分分别为 ![]() 甲、
甲、 ![]() 乙 , 则下列判断正确的是( )
乙 , 则下列判断正确的是( ) 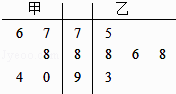
A.![]() 甲<
甲< ![]() 乙 , 甲比乙成绩稳定
乙 , 甲比乙成绩稳定
B.![]() 甲>
甲> ![]() 乙,甲比乙成绩稳定
乙,甲比乙成绩稳定
C.![]() 甲<
甲< ![]() 乙 , 乙比甲成绩稳定
乙 , 乙比甲成绩稳定
D.![]() 甲>
甲> ![]() 乙 , 乙比甲成绩稳定
乙 , 乙比甲成绩稳定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和最低点分别为(x0 , 2),(x0+
)的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和最低点分别为(x0 , 2),(x0+ ![]() ,﹣2).
,﹣2).
(1)求函数y=f(x)的解析式和单调递增区间;
(2)若当0≤x≤ ![]() 时,方程f(x)﹣m=0有两个不同的实数根α,β,试讨论α+β的值.
时,方程f(x)﹣m=0有两个不同的实数根α,β,试讨论α+β的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lg ![]() . (Ⅰ)求函数f(x)的定义域,并证明其在定义域上是奇函数;
. (Ⅰ)求函数f(x)的定义域,并证明其在定义域上是奇函数;
(Ⅱ)对于x∈[2,6],f(x)>lg ![]() 恒成立,求m的取值范围.
恒成立,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某算法的程序框图如图所示,若将输出(x,y)的值依次记(x1 , y1),(x2 , y2),…(xn , yn), 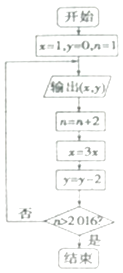
(1)若程序运行中输出的一个数组是(9,t),求t的值;
(2)程序结束时,共输出(x,y)的组数位多少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com