
【题目】已知等比数列![]() 的首项
的首项![]() ,数列
,数列![]() 前
前![]() 项和记为
项和记为![]() ,前
,前![]() 项积记为
项积记为![]() .
.
(1) 若![]() ,求等比数列
,求等比数列![]() 的公比
的公比![]() ;
;
(2) 在(1)的条件下,判断![]() 与
与![]() 的大小;并求
的大小;并求![]() 为何值时,
为何值时,![]() 取得最大值;
取得最大值;
(3) 在(1)的条件下,证明:若数列![]() 中的任意相邻三项按从小到大排列,则总可以使其成等差数列;若所有这些等差数列的公差按从小到大的顺序依次记为
中的任意相邻三项按从小到大排列,则总可以使其成等差数列;若所有这些等差数列的公差按从小到大的顺序依次记为![]() ,则数列
,则数列![]() 为等比数列.
为等比数列.
【答案】(1)![]() ;(2)
;(2)![]() ,当
,当![]() 时,
时,![]() 最大;(3)证明见解析.
最大;(3)证明见解析.
【解析】
(1)![]() ,求
,求![]() 和通项公式;
和通项公式;
(2)根据定义可知![]() ,然后根据公式
,然后根据公式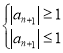 求
求![]() ,即
,即![]() 时
时![]() 的最大值,再根据
的最大值,再根据![]() ,判断
,判断![]() 的最大值;
的最大值;
(3)由(1)可知当![]() 为奇数时,
为奇数时,![]() 中的任意相邻三项由小到大排列是
中的任意相邻三项由小到大排列是![]() ,若成等差数列,可求
,若成等差数列,可求![]() 是否成立,并求公差,当
是否成立,并求公差,当![]() 是偶数时,设
是偶数时,设![]() 中的任意相邻三项按从小到大排列为
中的任意相邻三项按从小到大排列为![]() ,判断是否成等差数列,并求公差,并按定义判断数列
,判断是否成等差数列,并求公差,并按定义判断数列![]() 是否为等比数列
是否为等比数列
(1) ![]() ,解得
,解得![]() ,
,![]() ;
;
(2)![]() .又
.又![]() ,
,
![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.![]() 当
当![]() 时,
时,![]() 取得最大值,
取得最大值,
又![]() ,∴
,∴![]() 的最大值是
的最大值是![]() 和
和![]() 中的较大者,
中的较大者,
又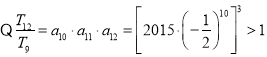 ,
,![]() .因此当
.因此当![]() 时,
时,![]() 最大.
最大.
(3)![]() ,
,![]() 随
随![]() 增大而减小,
增大而减小,![]() 奇数项均正,偶数项均负,
奇数项均正,偶数项均负,
①当![]() 是奇数时,设
是奇数时,设![]() 中的任意相邻三项按从小到大排列为
中的任意相邻三项按从小到大排列为![]() ,
,
则![]() ,
,![]() ,
,
![]() ,因此
,因此![]() 成等差数列,
成等差数列,
公差![]() ;
;
②当![]() 是偶数时,设
是偶数时,设![]() 中的任意相邻三项按从小到大排列为
中的任意相邻三项按从小到大排列为![]() ,
,
则![]() ,
,![]() .
.
∴![]() ,因此
,因此![]() 成等差数列,
成等差数列,
公差![]() ,
,
综上可知,![]() 中的任意相邻三项按从小到大排列,总可以使其成等差数列,
中的任意相邻三项按从小到大排列,总可以使其成等差数列,
且![]() , ∵
, ∵![]() ,∴数列
,∴数列![]() 为等比数列.
为等比数列.


科目:高中数学 来源: 题型:
【题目】田忌赛马是《史记》中记载的一个故事,说的是齐国大将军田忌经常与齐国众公子赛马,孙膑发现田忌的马和其他人的马相差并不远,都分为上、中、下三等.于是孙膑给田忌将军献策:比赛即将开始时,他让田忌用下等马对战公子们的上等马,用上等马对战公子们的中等马,用中等马对战公子们的下等马,从而使田忌赢得了许多赌注.假设田忌的各等级马与某公子的各等级马进行一场比赛,田忌获胜的概率如下表所示:
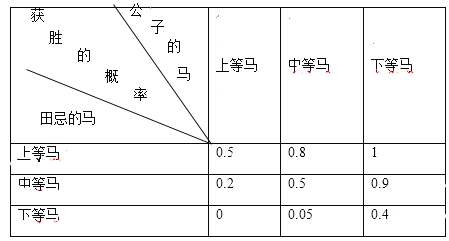
比赛规则规定:一次比赛由三场赛马组成,每场由公子和田忌各出一匹马参赛,结果只有胜和负两种,并且毎一方三场赛马的马的等级各不相同,三场比赛中至少获胜两场的一方为最终胜利者.
(1)如果按孙膑的策略比赛一次,求田忌获胜的概率;
(2)如果比赛约定,只能同等级马对战,每次比赛赌注1000金,即胜利者赢得对方1000金,每月比赛一次,求田忌一年赛马获利的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 焦点为
焦点为![]() ,
,![]() 为抛物线上在第一象限内一点,
为抛物线上在第一象限内一点,![]() 为原点,
为原点,![]() 面积为
面积为![]() .
.
(1)求抛物线方程;
(2)过![]() 点作两条直线分别交抛物线于异于点
点作两条直线分别交抛物线于异于点![]() 的两点
的两点![]() ,
,![]() ,且两直线斜率之和为
,且两直线斜率之和为![]() ,
,
(i)若![]() 为常数,求证直线
为常数,求证直线![]() 过定点
过定点![]() ;
;
(ii)当![]() 改变时,求(i)中距离
改变时,求(i)中距离![]() 最近的点
最近的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S-ABCD中,底面ABCD为直角梯形,AD//BC,∠SAD =∠DAB=![]() ,SA=3,SB=5,
,SA=3,SB=5,![]() ,
,![]() ,
,![]() .
.
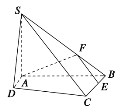
(1)求证:AB![]() 平面SAD;
平面SAD;
(2)求平面SCD与平面SAB所成的锐二面角的余弦值;
(3)点E,F分别为线段BC,SB上的一点,若平面AEF//平面SCD,求三棱锥B-AEF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学的甲、乙、丙三名同学参加高校自主招生考试,每位同学彼此独立的从![]() 四所高校中选2所.
四所高校中选2所.
(Ⅰ)求甲、乙、丙三名同学都选![]() 高校的概率;
高校的概率;
(Ⅱ)若已知甲同学特别喜欢![]() 高校,他必选
高校,他必选![]() 校,另在
校,另在![]() 三校中再随机选1所;而同学乙和丙对四所高校没有偏爱,因此他们每人在四所高校中随机选2所.
三校中再随机选1所;而同学乙和丙对四所高校没有偏爱,因此他们每人在四所高校中随机选2所.
(ⅰ)求甲同学选![]() 高校且乙、丙都未选
高校且乙、丙都未选![]() 高校的概率;
高校的概率;
(ⅱ)记![]() 为甲、乙、丙三名同学中选
为甲、乙、丙三名同学中选![]() 校的人数,求随机变量
校的人数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知矩形![]() ,
,![]() ,
,![]() ,将
,将![]() 沿对角线
沿对角线![]() 进行翻折,得到三棱锥
进行翻折,得到三棱锥![]() ,则在翻折的过程中,有下列结论正确的有_____.
,则在翻折的过程中,有下列结论正确的有_____.
①三棱锥![]() 的体积的最大值为
的体积的最大值为![]() ;
;
②三棱锥![]() 的外接球体积不变;
的外接球体积不变;
③三棱锥![]() 的体积最大值时,二面角
的体积最大值时,二面角![]() 的大小是60°;
的大小是60°;
④异面直线![]() 与
与![]() 所成角的最大值为90°.
所成角的最大值为90°.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知圆
中,已知圆![]() 与直线
与直线![]() 相切,点A为圆
相切,点A为圆![]() 上一动点,
上一动点,![]() 轴于点N,且动点满足
轴于点N,且动点满足![]() ,设动点M的轨迹为曲线C.
,设动点M的轨迹为曲线C.
(1)求曲线C的方程;
(2)设P,Q是曲线C上两动点,线段![]() 的中点为T,
的中点为T,![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() .点
.点![]() 、
、![]() 、
、![]() 分别为棱
分别为棱![]() 、
、![]() 、
、![]() 的中点,
的中点,![]() 是线段
是线段![]() 的中点,
的中点,![]() ,
,![]() .
.
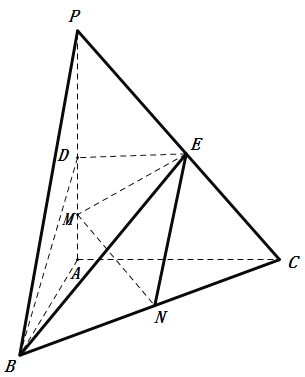
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)已知点![]() 在棱
在棱![]() 上,且直线
上,且直线![]() 与直线
与直线![]() 所成角的余弦值为
所成角的余弦值为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com